Ejercita tu mente con la lógica proposicional matemática
¿Alguna vez te has preguntado cómo los matemáticos resuelven problemas complejos con facilidad? La respuesta es simple: a través de la lógica proposicional matemática. Esta rama de la matemática se enfoca en la estructura lógica de los argumentos, y cómo se pueden representar matemáticamente para analizarlos y resolverlos.
En este artículo, exploraremos la lógica proposicional matemática y cómo puedes ejercitar tu mente a través de ella.
¿Qué es la lógica proposicional matemática?
La lógica proposicional matemática es una rama de la matemática que se enfoca en la estructura lógica de los argumentos. Se basa en la manipulación de proposiciones, que son declaraciones que pueden ser verdaderas o falsas.
La lógica proposicional matemática se enfoca en representar estas proposiciones como símbolos matemáticos, y luego manipularlos de acuerdo con las reglas de la lógica para llegar a conclusiones lógicas.
Ejemplo:
Supongamos que queremos representar la proposición "si llueve, entonces no salgo de casa" usando la lógica proposicional matemática. Podemos representarla como p → ¬q, donde p representa "llueve" y q representa "salgo de casa".
Esta representación nos permite manipular la proposición y llegar a conclusiones lógicas. Por ejemplo, si sabemos que p es verdadero, entonces podemos concluir que ¬q también es verdadero.
Cómo ejercitar tu mente con la lógica proposicional matemática
La lógica proposicional matemática es una excelente manera de ejercitar tu mente y mejorar tus habilidades de razonamiento. Aquí hay algunas formas de hacerlo:
1. Resuelve problemas de lógica
Los problemas de lógica son una excelente manera de ejercitar tu mente y mejorar tus habilidades de razonamiento. Estos problemas te desafían a encontrar soluciones lógicas a situaciones complejas, y a menudo requieren el uso de la lógica proposicional matemática.
2. Practica la representación simbólica de proposiciones
La representación simbólica de proposiciones es una habilidad clave en la lógica proposicional matemática. Practicar la representación simbólica de proposiciones te ayudará a mejorar tu habilidad para manipular proposiciones y llegar a conclusiones lógicas.
3. Crea tablas de verdad
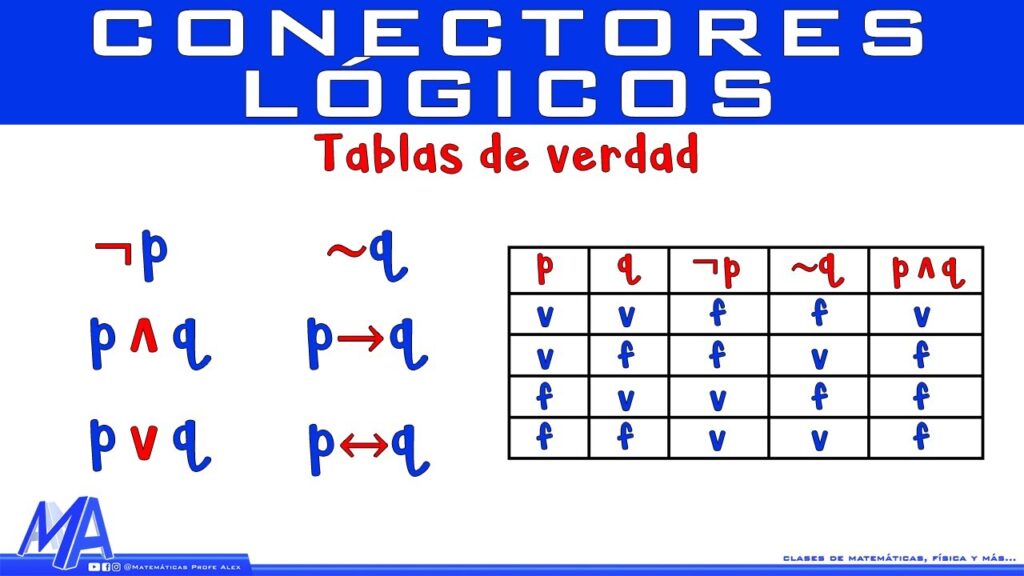
Las tablas de verdad son una herramienta útil en la lógica proposicional matemática. Te permiten representar todas las posibles combinaciones de valores de verdad para una proposición dada, lo que puede ayudarte a llegar a conclusiones lógicas.
4. Estudia la lógica proposicional matemática
La lógica proposicional matemática es una materia compleja, pero estudiarla puede ayudarte a mejorar tus habilidades de razonamiento. Hay muchos recursos disponibles en línea y en las bibliotecas para aprender sobre la lógica proposicional matemática.
Conclusión
La lógica proposicional matemática es una herramienta poderosa para ejercitar tu mente y mejorar tus habilidades de razonamiento. A través de la manipulación de proposiciones y la representación simbólica, puedes llegar a conclusiones lógicas y resolver problemas complejos con facilidad.
Preguntas frecuentes
1. ¿Qué es una proposición?
Una proposición es una declaración que puede ser verdadera o falsa.
2. ¿Por qué es importante la lógica proposicional matemática?
La lógica proposicional matemática es importante porque te permite representar proposiciones como símbolos matemáticos y manipularlos para llegar a conclusiones lógicas.
3. ¿Qué son las tablas de verdad?
Las tablas de verdad son una herramienta en la lógica proposicional matemática que te permiten representar todas las posibles combinaciones de valores de verdad para una proposición dada.
4. ¿Cómo puedo mejorar mis habilidades de lógica proposicional matemática?
Puedes mejorar tus habilidades de lógica proposicional matemática resolviendo problemas de lógica, practicando la representación simbólica de proposiciones, creando tablas de verdad y estudiando la materia.
5. ¿Qué es la implicación en la lógica proposicional matemática?
La implicación es una relación entre dos proposiciones, en la que la verdad de una proposición implica la verdad de la otra. En la lógica proposicional matemática, la implicación se representa como p → q, donde p y q son proposiciones.
Deja una respuesta