Lógica proposicional: la base de la inteligencia artificial
La inteligencia artificial es una rama de la informática que busca crear sistemas capaces de realizar tareas que requieren inteligencia humana, como el aprendizaje, la resolución de problemas y la toma de decisiones. Para lograr esto, la inteligencia artificial se basa en diferentes áreas de la matemática, la estadística y la lógica, siendo la lógica proposicional una de las más importantes.
¿Qué es la lógica proposicional?
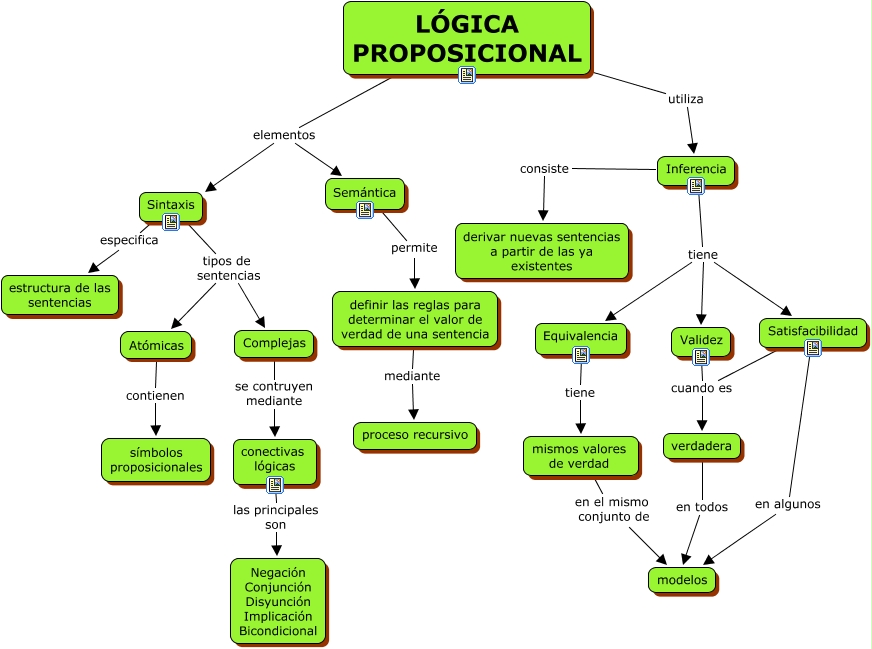
La lógica proposicional es una rama de la lógica que estudia las proposiciones y las operaciones que se pueden realizar con ellas. Una proposición es una afirmación que puede ser verdadera o falsa, como “hoy es lunes” o “todos los gatos son mamíferos”. La lógica proposicional se encarga de analizar cómo se relacionan estas proposiciones entre sí y cómo se pueden combinar para formar argumentos.
¿Por qué es importante la lógica proposicional en la inteligencia artificial?
La lógica proposicional es importante en la inteligencia artificial porque permite modelar el conocimiento y el razonamiento humano de una manera formal y precisa. En otras palabras, la lógica proposicional permite definir cómo se relacionan las diferentes proposiciones que se utilizan en un sistema de inteligencia artificial y cómo se pueden deducir nuevas proposiciones a partir de las existentes.
Por ejemplo, si queremos que un sistema de inteligencia artificial sea capaz de reconocer si una imagen contiene un gato, podemos definir una serie de proposiciones que describan las características que debe tener un gato, como “tiene cuatro patas”, “tiene pelo”, “tiene bigotes”, entre otras. Luego, utilizando las operaciones lógicas de la lógica proposicional, podemos combinar estas proposiciones para deducir si una imagen contiene o no un gato.
Operaciones lógicas en la lógica proposicional
En la lógica proposicional existen diferentes operaciones que se pueden realizar con proposiciones, como la negación, la conjunción, la disyunción, la implicación y la equivalencia.
- Negación: la negación de una proposición se representa con el símbolo ¬ y se utiliza para indicar que una proposición es falsa. Por ejemplo, la negación de la proposición “hoy es lunes” sería “hoy no es lunes”.
- Conjunción: la conjunción de dos proposiciones se representa con el símbolo ∧ y se utiliza para indicar que ambas proposiciones son verdaderas. Por ejemplo, la conjunción de las proposiciones “hoy es lunes” y “estoy trabajando” sería “hoy es lunes ∧ estoy trabajando”.
- Disyunción: la disyunción de dos proposiciones se representa con el símbolo ∨ y se utiliza para indicar que al menos una de las proposiciones es verdadera. Por ejemplo, la disyunción de las proposiciones “hoy es lunes” y “hoy es martes” sería “hoy es lunes ∨ hoy es martes”.
- Implicación: la implicación de dos proposiciones se representa con el símbolo → y se utiliza para indicar que si la primera proposición es verdadera, entonces la segunda también lo es. Por ejemplo, la implicación de las proposiciones “si llueve, me quedo en casa” y “está lloviendo” sería “si llueve → me quedo en casa”.
- Equivalencia: la equivalencia de dos proposiciones se representa con el símbolo ↔ y se utiliza para indicar que ambas proposiciones son verdaderas o falsas al mismo tiempo. Por ejemplo, la equivalencia de las proposiciones “hoy es lunes” y “mañana es martes” sería “hoy es lunes ↔ mañana es martes”.
Lógica proposicional y sistemas expertos
Los sistemas expertos son un tipo de sistema de inteligencia artificial que se basan en el conocimiento de expertos en una determinada área para realizar tareas específicas. Estos sistemas utilizan la lógica proposicional para representar el conocimiento y el razonamiento de los expertos de manera formal y precisa.
Por ejemplo, si queremos crear un sistema experto para diagnosticar enfermedades, podemos utilizar la lógica proposicional para representar las diferentes síntomas y enfermedades, y las relaciones que existen entre ellas. Luego, utilizando las operaciones lógicas de la lógica proposicional, podemos deducir cuál es la enfermedad más probable a partir de los síntomas que presenta el paciente.
Conclusión
La lógica proposicional es una herramienta fundamental en la inteligencia artificial, ya que permite modelar el conocimiento y el razonamiento humano de una manera formal y precisa. A través de las operaciones lógicas de la lógica proposicional, podemos combinar proposiciones para deducir nuevas proposiciones y realizar tareas complejas como el reconocimiento de imágenes o el diagnóstico de enfermedades.
Preguntas frecuentes
1. ¿Qué es una proposición en la lógica proposicional?
Una proposición es una afirmación que puede ser verdadera o falsa, como “hoy es lunes” o “todos los gatos son mamíferos”. En la lógica proposicional, las proposiciones se utilizan como elementos básicos para construir argumentos.
2. ¿Qué operaciones lógicas existen en la lógica proposicional?
En la lógica proposicional existen diferentes operaciones lógicas, como la negación, la conjunción, la disyunción, la implicación y la equivalencia. Estas operaciones se utilizan para combinar proposiciones y deducir nuevas proposiciones.
3. ¿Qué son los sistemas expertos?
Los sistemas expertos son un tipo de sistema de inteligencia artificial que se basan en el conocimiento de expertos en una determinada área para realizar tareas específicas. Estos sistemas utilizan la lógica proposicional para representar el conocimiento y el razonamiento de los expertos de manera formal y precisa.
4. ¿Cómo se utiliza la lógica proposicional en el reconocimiento de imágenes?
En el reconocimiento de imágenes, la lógica proposicional se utiliza para definir las características que deben tener los objetos que se quieren reconocer, como los gatos o los perros. Luego, utilizando las operaciones lógicas de la lógica proposicional, se pueden combinar estas características para deducir si una imagen contiene o no un objeto específico.
5. ¿Qué es la implicación en la lógica proposicional?
La implicación en la lógica proposicional es una operación que se utiliza para indicar que si la primera proposición es verdadera, entonces la segunda también lo es. Por ejemplo, la implicación de las proposiciones “si llueve, me quedo en casa” y “está lloviendo” sería “si llueve → me quedo en casa”.
Deja una respuesta