Descubre la lógica proposicional: explicación clara y sencilla

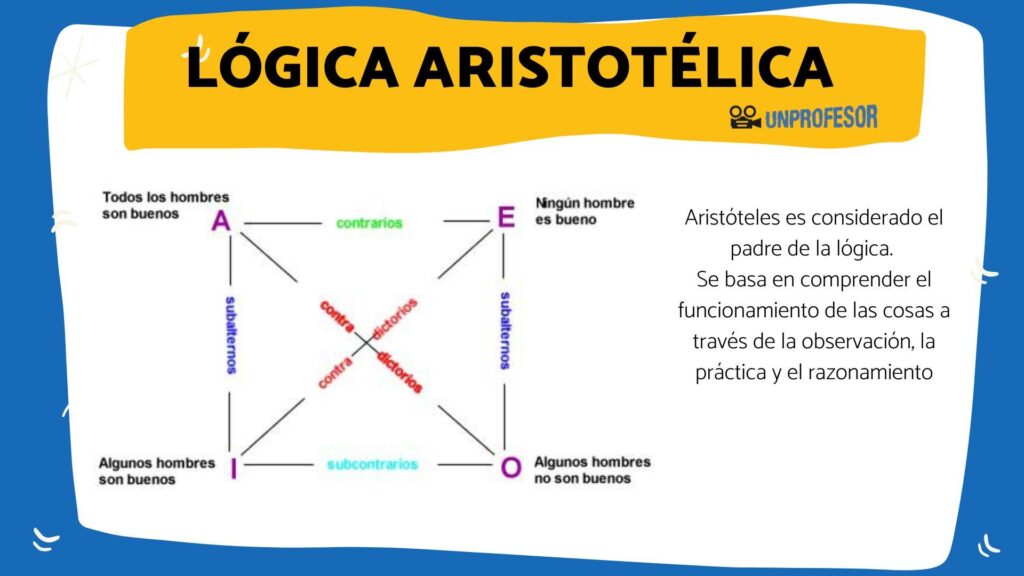
La lógica proposicional es una rama de la lógica que se encarga de estudiar el razonamiento mediante proposiciones. Una proposición es una afirmación que puede ser verdadera o falsa, y la lógica proposicional se encarga de analizar cómo se relacionan las proposiciones entre sí.

En este artículo, te explicaremos de manera clara y sencilla qué es la lógica proposicional y cómo funciona.

¿Qué es una proposición?

Como mencionamos anteriormente, una proposición es una afirmación que puede ser verdadera o falsa. Por ejemplo, "El cielo es azul" es una proposición, ya que puede ser verdadera o falsa dependiendo de las condiciones climáticas.

Conectores lógicos

La lógica proposicional utiliza conectores lógicos para relacionar proposiciones. Los conectores lógicos más comunes son:

• Negación: se utiliza para negar una proposición. Por ejemplo, si la proposición es "El cielo es azul", la negación sería "El cielo no es azul".
• Conjunción: se utiliza para unir dos proposiciones. La conjunción se representa con el símbolo "y". Por ejemplo, "El cielo es azul y el sol está brillando".
• Disyunción: se utiliza para indicar que al menos una de dos proposiciones es verdadera. La disyunción se representa con el símbolo "o". Por ejemplo, "Voy a comer una pizza o una ensalada".
• Implicación: se utiliza para indicar que una proposición implica otra. La implicación se representa con el símbolo "→". Por ejemplo, "Si estudio, entonces sacaré buenas notas".
• Equivocación: se utiliza para indicar que dos proposiciones son equivalentes. La equivocación se representa con el símbolo "↔". Por ejemplo, "El cielo es azul si y solo si no está nublado".

Tablas de verdad

Las tablas de verdad son una herramienta que se utiliza en la lógica proposicional para analizar la relación entre proposiciones. En una tabla de verdad, se listan todas las posibles combinaciones de valores de verdad para las proposiciones involucradas en una expresión lógica.

Por ejemplo, si tenemos la expresión "p → q", se deben considerar las cuatro posibles combinaciones de valores de verdad para "p" y "q": (1) p es verdadero y q es verdadero, (2) p es verdadero y q es falso, (3) p es falso y q es verdadero, y (4) p es falso y q es falso. Se asigna un valor de verdad a la expresión "p → q" para cada una de estas combinaciones, y se construye una tabla que resume los resultados.

Aplicaciones de la lógica proposicional

La lógica proposicional tiene aplicaciones en diversas áreas, como la informática, la filosofía y las matemáticas. En informática, la lógica proposicional se utiliza para la programación de algoritmos y la creación de sistemas de inteligencia artificial. En filosofía, la lógica proposicional se utiliza para analizar argumentos y establecer la validez de razonamientos. En matemáticas, la lógica proposicional se utiliza para el análisis de proposiciones matemáticas y la resolución de problemas.

Conclusión

La lógica proposicional es una herramienta importante para el análisis y el razonamiento. Conociendo los conectores lógicos y las tablas de verdad, es posible analizar la relación entre proposiciones y establecer la validez de razonamientos. La lógica proposicional tiene aplicaciones en diversas áreas y es una habilidad útil para desarrollar tanto en la vida cotidiana como en el ámbito académico y profesional.

Preguntas frecuentes

¿Qué diferencia hay entre la lógica proposicional y la lógica de predicados?

La lógica proposicional se encarga del análisis de proposiciones simples, mientras que la lógica de predicados se encarga del análisis de proposiciones complejas que involucran variables y cuantificadores.

¿Cómo se representan las proposiciones en la lógica proposicional?

Las proposiciones se representan con variables proposicionales, que suelen ser letras minúsculas como "p" o "q".

¿Cuál es la importancia de la lógica proposicional en la programación de computadoras?

La lógica proposicional es esencial en la creación de algoritmos y sistemas de inteligencia artificial, ya que permite establecer reglas y condiciones para la toma de decisiones.

¿Qué es una contradicción en la lógica proposicional?

Una contradicción es una expresión lógica que es siempre falsa, independientemente de los valores de verdad de las proposiciones involucradas.

¿Qué es una tautología en la lógica proposicional?

Una tautología es una expresión lógica que es siempre verdadera, independientemente de los valores de verdad de las proposiciones involucradas.