Descubre la lógica matemática de si y solo si en simples pasos
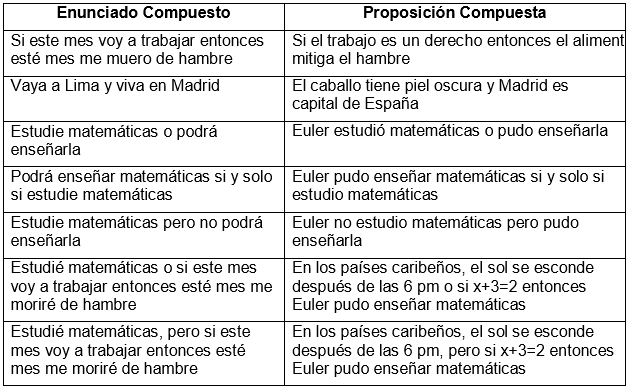
La lógica matemática es una herramienta esencial en el mundo de las matemáticas y la informática. Si alguna vez has estudiado lógica, probablemente hayas encontrado la expresión "si y solo si" o "solo si" en tus lecciones. Estas expresiones son fundamentales para comprender la lógica matemática, pero pueden ser un poco difíciles de entender al principio. En este artículo, te explicaremos en simples pasos la lógica matemática de "si y solo si".
¿Qué significa "si y solo si"?
"Si y solo si" es una expresión utilizada en lógica matemática para indicar que dos enunciados son equivalentes. Esto significa que si uno de los enunciados es verdadero, entonces el otro también lo es, y si uno es falso, entonces el otro también lo es. La expresión "si y solo si" se abrevia comúnmente como "ssi".
¿Cómo se representa "si y solo si" en lógica matemática?
En lógica matemática, "si y solo si" se representa con el símbolo "≡", que se lee como "es equivalente a". Por lo tanto, si tenemos dos enunciados, p y q, podemos escribir su equivalencia como:
p ≡ q
Esto significa que "p si y solo si q".
¿Cómo se usa "si y solo si" en lógica matemática?
Para entender cómo se usa "si y solo si" en lógica matemática, es útil considerar algunos ejemplos.
Supongamos que tenemos dos enunciados: "si llueve, entonces el suelo está mojado" y "el suelo está mojado solo si llueve". Estos dos enunciados son equivalentes, ya que si llueve, entonces el suelo estará mojado, y si el suelo está mojado, entonces necesariamente ha llovido. Por lo tanto, podemos escribir:
llueve ≡ el suelo está mojado
Otro ejemplo es el siguiente: "un número es par si y solo si es divisible entre 2". Este enunciado es verdadero, ya que todos los números pares son divisibles entre 2, y todos los números divisibles entre 2 son pares. Por lo tanto, podemos escribir:
n es par ≡ n es divisible entre 2
¿Cómo se demuestra una equivalencia "si y solo si"?
Para demostrar que dos enunciados son equivalentes, es necesario demostrar que ambos enunciados son verdaderos o falsos al mismo tiempo. Por ejemplo, si queremos demostrar que "si llueve, entonces el suelo está mojado" es equivalente a "el suelo está mojado solo si llueve", podemos hacer lo siguiente:
- Si llueve, entonces el suelo estará mojado (primera afirmación).
- Si el suelo está mojado, entonces necesariamente ha llovido (segunda afirmación).
- Por lo tanto, si llueve, entonces el suelo está mojado, y si el suelo está mojado, entonces necesariamente ha llovido (ambas afirmaciones son verdaderas al mismo tiempo).
- Por lo tanto, "si llueve, entonces el suelo está mojado" es equivalente a "el suelo está mojado solo si llueve".
¿Cómo se usa "si y solo si" en matemáticas?
En matemáticas, "si y solo si" se utiliza para definir conceptos. Por ejemplo, podemos definir un número primo como un número entero positivo que solo es divisible entre 1 y sí mismo. Podemos escribir esta definición como:
n es primo ≡ n es un número entero positivo y solo es divisible entre 1 y n
Otra forma común en que se usa "si y solo si" en matemáticas es en las demostraciones. Si queremos demostrar que dos cosas son iguales, podemos demostrar que son equivalentes "si y solo si". Por ejemplo, si queremos demostrar que dos fracciones son iguales, podemos demostrar que sus numeradores y denominadores son equivalentes "si y solo si".
Conclusión
La lógica matemática de "si y solo si" es fundamental para la comprensión de las matemáticas y la informática. Esta expresión se utiliza para indicar que dos enunciados son equivalentes, lo que significa que si uno de los enunciados es verdadero, entonces el otro también lo es, y si uno es falso, entonces el otro también lo es. Para demostrar una equivalencia "si y solo si", es necesario demostrar que ambos enunciados son verdaderos o falsos al mismo tiempo.
Preguntas frecuentes
1. ¿Qué significa "si y solo si" en matemáticas?
"Si y solo si" en matemáticas significa que dos cosas son equivalentes, lo que significa que si una cosa es verdadera, entonces la otra también lo es, y si una cosa es falsa, entonces la otra también lo es.
2. ¿Cómo se representa "si y solo si" en lógica matemática?
En lógica matemática, "si y solo si" se representa con el símbolo "≡", que se lee como "es equivalente a".
3. ¿Cómo se demuestra una equivalencia "si y solo si"?
Para demostrar una equivalencia "si y solo si", es necesario demostrar que ambos enunciados son verdaderos o falsos al mismo tiempo.
4. ¿Cómo se usa "si y solo si" en matemáticas?
"Si y solo si" se utiliza en matemáticas para definir conceptos y para demostrar que dos cosas son iguales.
5. ¿Qué es un ejemplo de "si y solo si" en matemáticas?
Un ejemplo de "si y solo si" en matemáticas es la definición de un número primo como un número entero positivo que solo es divisible entre 1 y sí mismo. Podemos escribir esta definición como: "n es primo ≡ n es un número entero positivo y solo es divisible entre 1 y n".
Deja una respuesta