La lógica según expertos: definiciones esenciales

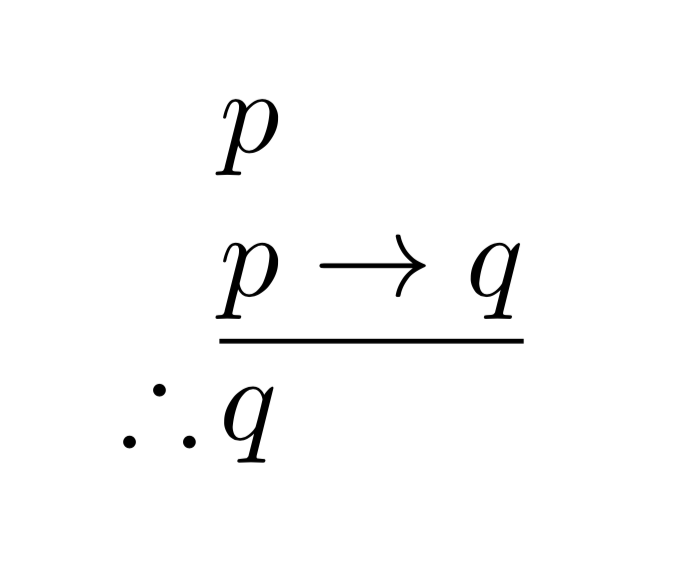
La lógica es una disciplina fundamental en la filosofía y en la vida en general. Se trata de una herramienta que nos permite razonar de manera coherente y llegar a conclusiones precisas. Pero, ¿qué es exactamente la lógica? ¿Qué conceptos esenciales debemos conocer para comprenderla mejor? En este artículo, te presentamos las definiciones esenciales de la lógica según expertos en la materia.

1. ¿Qué es la lógica?

La lógica es la disciplina que estudia el razonamiento y la argumentación. Su objetivo es establecer reglas y principios que nos permitan distinguir un razonamiento válido de uno inválido. En otras palabras, la lógica nos ayuda a discernir entre lo que es verdadero y lo que no lo es.

2. Proposiciones

Una proposición es una afirmación que puede ser verdadera o falsa. En lógica, las proposiciones se representan mediante letras minúsculas (p, q, r, etc.). Por ejemplo, la proposición "el cielo es azul" puede representarse como p.

3. Conectores lógicos

Los conectores lógicos son palabras o símbolos que se utilizan para unir proposiciones y formar argumentos más complejos. Los conectores más comunes son:

• Conjunción: se representa por el símbolo ∧ o por la palabra "y". Por ejemplo, la proposición p ∧ q significa "p y q".
• Disyunción: se representa por el símbolo ∨ o por la palabra "o". Por ejemplo, la proposición p ∨ q significa "p o q".
• Negación: se representa por el símbolo ¬ o por la palabra "no". Por ejemplo, la proposición ¬p significa "no p".
• Implicación: se representa por el símbolo → o por la palabra "si... entonces". Por ejemplo, la proposición p → q significa "si p entonces q".

4. Argumentos

Un argumento es un conjunto de proposiciones que se presentan como evidencia para apoyar una conclusión. En un argumento, las proposiciones que se presentan como evidencia se llaman premisas, y la proposición que se pretende demostrar se llama conclusión. Un argumento válido es aquel en el que, si todas las premisas son verdaderas, la conclusión también lo será.

5. Falacias

Una falacia es un error de razonamiento que se comete al argumentar. Hay diversos tipos de falacias, pero algunas de las más comunes son:

• Falacia ad hominem: consiste en atacar al argumentador en lugar de refutar sus argumentos.
• Falacia de la pendiente resbaladiza: consiste en afirmar que si se permite una cosa, entonces se tendrán que permitir otras cosas extremas.
• Falacia de la petición de principio: consiste en asumir como verdadero lo que se pretende demostrar.

6. Silogismos

Un silogismo es un argumento que consta de dos premisas y una conclusión. Las premisas y la conclusión se relacionan mediante los llamados términos del silogismo: el término mayor (que aparece en la premisa mayor), el término menor (que aparece en la premisa menor) y el término medio (que aparece en ambas premisas).

7. Demostración

Una demostración es un argumento que tiene la particularidad de ser válido y de tener todas sus premisas verdaderas. En otras palabras, una demostración es un argumento que nos permite conocer algo con certeza.

8. Inducción

La inducción es un tipo de razonamiento que se basa en la observación de casos particulares para llegar a una conclusión general. Por ejemplo, si hemos visto que todos los cisnes que hemos observado son blancos, podemos concluir que todos los cisnes son blancos.

9. Deducción

La deducción es un tipo de razonamiento que se basa en la aplicación de reglas lógicas para llegar a una conclusión a partir de premisas verdaderas. Por ejemplo, si sabemos que todos los hombres son mortales y que Sócrates es un hombre, podemos deducir que Sócrates es mortal.

10. Paradojas

Una paradoja es una situación en la que se llega a una conclusión que parece contradictoria o imposible. Por ejemplo, la paradoja del mentiroso es la siguiente afirmación: "Esta frase es falsa". Si afirmamos que la frase es verdadera, entonces estamos diciendo que es falsa, y si afirmamos que es falsa, entonces estamos diciendo que es verdadera.

11. Teoremas

Un teorema es una proposición que se ha demostrado que es verdadera a partir de otras proposiciones verdaderas. Los teoremas son fundamentales en las matemáticas y en la lógica, ya que nos permiten establecer verdades universales a partir de verdades particulares.

12. Axiomas

Un axioma es una proposición que se acepta como verdadera sin necesidad de demostración. Los axiomas son fundamentales en la lógica y en las matemáticas, ya que nos permiten establecer una base sólida sobre la cual construir teoremas y demostraciones.

13. Paradoja de Russell

La paradoja de Russell es una paradoja que se presenta en la teoría de conjuntos. Según esta paradoja, no es posible construir un conjunto que contenga a todos los conjuntos que no se contienen a sí mismos. Esta paradoja ha sido objeto de numerosos debates y ha llevado a la formulación de diversas teorías de conjuntos.

14. Falacia post hoc

La falacia post hoc consiste en afirmar que, porque una cosa ha ocurrido después de otra, la primera cosa es la causa de la segunda. Por ejemplo, si una persona se cura de una enfermedad después de tomar un remedio, no necesariamente significa que el remedio haya sido la causa de la curación.

15. Paradoja de Epiménides

La paradoja de Epiménides es una paradoja que se presenta en la lógica. Según esta paradoja, si un cretense afirma que todos los cretenses son mentirosos, ¿debemos creerle o no? Si le creemos, entonces estamos aceptando que los cretenses son mentirosos, lo cual incluye al propio cretense que nos está hablando. Pero si no le creemos, entonces estamos contradiciendo su afirmación de que todos los cretenses son mentirosos.

Conclusión

La lógica es una disciplina fundamental en la filosofía y en la vida en general. En este artículo, hemos repasado algunas de las definiciones esenciales de la lógica según expertos en la materia, como las proposiciones, los conectores lógicos, los argumentos, las falacias, los silogismos, las demo