Descubre la lógica detrás de los números complejos

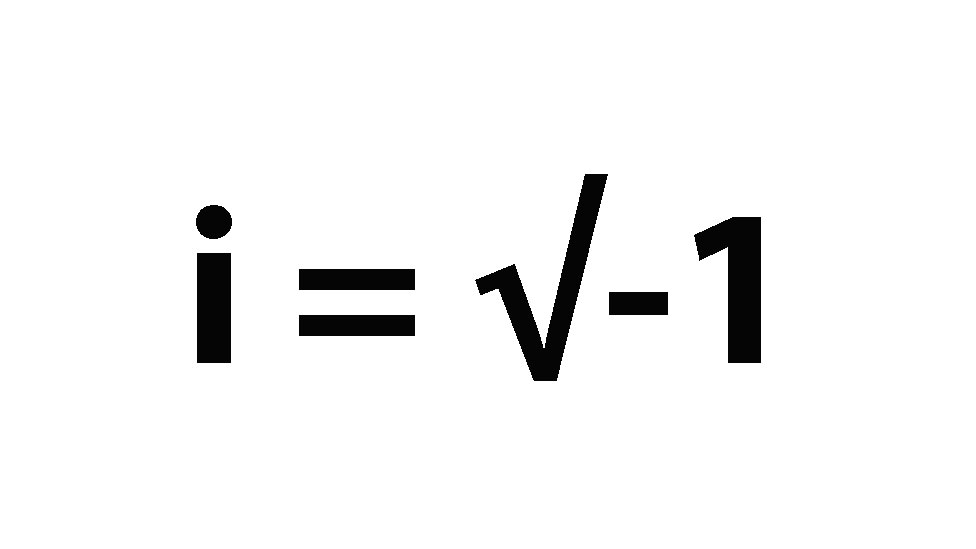
Los números complejos son una extensión de los números reales en la que se introduce la unidad imaginaria "i", la cual se define como la raíz cuadrada de -1. Aunque estos números puedan parecer extraños al principio, su lógica y aplicación son fundamentales en muchas áreas de la ciencia y la tecnología.

En este artículo, exploraremos la lógica detrás de los números complejos y veremos cómo se utilizan en el mundo real.

¿Qué son los números complejos?

Los números complejos se definen como una combinación lineal de un número real y un número imaginario. Es decir, un número complejo se puede escribir como a + bi, donde "a" y "b" son números reales y "i" es la unidad imaginaria.

Es importante destacar que los números complejos no son sólo números imaginarios, sino una combinación de ambos. Por ejemplo, el número 3 + 2i es un número complejo, mientras que 2i no lo es.

¿Cómo se utilizan los números complejos?

Los números complejos se utilizan en varias áreas, como la física, la ingeniería y las matemáticas. En la física, los números complejos se utilizan para describir ondas electromagnéticas y fenómenos cuánticos. En la ingeniería, se utilizan para analizar circuitos eléctricos y sistemas de control. En las matemáticas, los números complejos se utilizan para resolver ecuaciones y para estudiar funciones complejas.

Operaciones con números complejos

Las operaciones básicas con números complejos son la suma, la resta, la multiplicación y la división. Para sumar o restar dos números complejos, se suman o restan las partes reales y las partes imaginarias por separado. Por ejemplo:

(2 + 3i) + (4 - 2i) = 6 + i
(2 + 3i) - (4 - 2i) = -2 + 5i

Para multiplicar dos números complejos, se utiliza la propiedad distributiva y se aplica la fórmula (a + bi)(c + di) = (ac - bd) + (ad + bc)i. Por ejemplo:

(2 + 3i)(4 - 2i) = 14 + 8i

Para dividir dos números complejos, se multiplica el numerador y el denominador por el conjugado del denominador y se simplifica. El conjugado de un número complejo a + bi es a - bi. Por ejemplo:

(2 + 3i)/(4 - 2i) = (2 + 3i)(4 + 2i)/(4^2 + 2^2) = (8 + 14i)/20 = 2/5 + 7/10i

Representación gráfica

Los números complejos se pueden representar gráficamente en un plano cartesiano, en el que el eje horizontal representa las partes reales y el eje vertical las partes imaginarias. Cada número complejo se representa por un punto en el plano.

Módulo y argumento

El módulo de un número complejo es la distancia del origen al punto que lo representa en el plano. El argumento es el ángulo formado por el número complejo y el eje horizontal.

Forma polar

Los números complejos también se pueden expresar en forma polar, que consiste en escribir el módulo y el argumento del número complejo. Por ejemplo, el número complejo 2 + 3i se puede escribir en forma polar como 3.6055∠56.31°.

Conclusión

Los números complejos son una herramienta fundamental en la ciencia y la tecnología, y su lógica y aplicación son de gran importancia. Aunque puedan parecer extraños al principio, los números complejos son una extensión natural de los números reales y su uso es cada vez más común en la vida cotidiana.

Preguntas frecuentes

1. ¿Por qué se utilizan los números complejos?

Los números complejos se utilizan en varias áreas, como la física, la ingeniería y las matemáticas, para describir fenómenos que no se pueden explicar con números reales.

2. ¿Cómo se suman y restan los números complejos?

Para sumar o restar dos números complejos, se suman o restan las partes reales y las partes imaginarias por separado.

3. ¿Cómo se multiplican los números complejos?

Para multiplicar dos números complejos, se utiliza la fórmula (a + bi)(c + di) = (ac - bd) + (ad + bc)i.

4. ¿Cómo se dividen los números complejos?

Para dividir dos números complejos, se multiplica el numerador y el denominador por el conjugado del denominador y se simplifica.

5. ¿Cómo se representan los números complejos gráficamente?

Los números complejos se pueden representar gráficamente en un plano cartesiano, en el que el eje horizontal representa las partes reales y el eje vertical las partes imaginarias. Cada número complejo se representa por un punto en el plano.