Descubre la altura en matemáticas: fórmulas y ejemplos

La altura es un concepto matemático fundamental que se utiliza en muchas áreas, desde la geometría hasta la trigonometría. En términos simples, la altura se define como la distancia vertical entre un punto y una línea base, y es una herramienta esencial para resolver muchos problemas matemáticos. En este artículo, exploraremos las fórmulas y ejemplos más comunes para calcular la altura en diferentes situaciones.

Conceptos básicos

Antes de sumergirnos en las fórmulas, es importante entender algunos conceptos básicos relacionados con la altura. En geometría, la altura se refiere a la línea perpendicular que se dibuja desde un vértice de un triángulo a su base. La base es la línea más larga en un triángulo, y la altura siempre se mide perpendicularmente a ella. En otras palabras, la altura es la distancia más corta entre el vértice y la base.

Cálculo de la altura en un triángulo

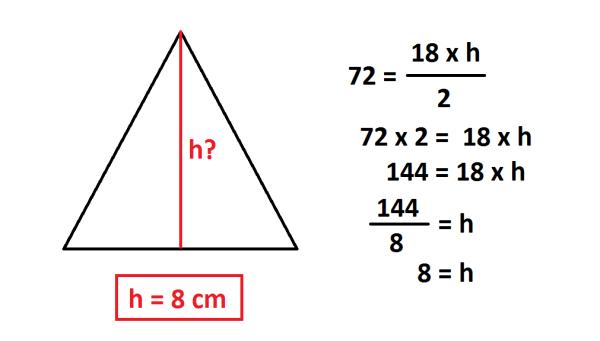
El cálculo de la altura en un triángulo es una de las aplicaciones más comunes de este concepto. La fórmula para encontrar la altura de un triángulo es la siguiente:

altura = (2 * área) / base

Donde el área es la mitad del producto de la base y la altura, y la base es la longitud de la línea que se dibuja desde un extremo del triángulo hasta el otro extremo que es perpendicular a la altura. Veamos un ejemplo:

Supongamos que tenemos un triángulo con una base de 6 cm y un área de 12 cm². ¿Cuál es la altura del triángulo?

altura = (2 * 12) / 6
altura = 4 cm

Por lo tanto, la altura del triángulo es de 4 cm.

Cálculo de la altura en un rectángulo

Otra aplicación común de la altura es en la geometría de un rectángulo. En un rectángulo, la altura es la línea perpendicular que se dibuja desde la base hasta el lado opuesto. La fórmula para encontrar la altura de un rectángulo es la siguiente:

altura = área / base

Donde el área es el producto de la base y la altura del rectángulo. Veamos un ejemplo:

Supongamos que tenemos un rectángulo con una base de 8 cm y un área de 32 cm². ¿Cuál es la altura del rectángulo?

altura = 32 / 8
altura = 4 cm

Por lo tanto, la altura del rectángulo es de 4 cm.

Cálculo de la altura en un prisma

La altura también se utiliza en la geometría de los prismas, que son sólidos con una base y caras laterales rectangulares o cuadradas. La fórmula para encontrar la altura de un prisma es la siguiente:

altura = volumen / área de la base

Donde el volumen es el producto del área de la base y la altura del prisma, y el área de la base es el área de la forma que se encuentra en la parte inferior del prisma. Veamos un ejemplo:

Supongamos que tenemos un prisma con una base cuadrada de 4 cm de lado, una altura de 6 cm y un volumen de 96 cm³. ¿Cuál es la altura del prisma?

área de la base = 4 * 4 = 16 cm²
altura = 96 / 16
altura = 6 cm

Por lo tanto, la altura del prisma es de 6 cm.

Cálculo de la altura en la trigonometría

Además de la geometría, la altura también se utiliza en la trigonometría. En este contexto, la altura se refiere a la altura de un triángulo rectángulo, que es la línea perpendicular que se dibuja desde el vértice opuesto al ángulo recto hasta la base. La altura también se puede referir a la altura de un objeto, como un edificio o una montaña, medida desde el nivel del suelo.

La fórmula para encontrar la altura de un triángulo rectángulo es la siguiente:

altura = seno (ángulo) * hipotenusa

Donde el seno del ángulo es la relación entre el lado opuesto al ángulo y la hipotenusa. La hipotenusa es el lado más largo en un triángulo rectángulo y se encuentra opuesto al ángulo recto. Veamos un ejemplo:

Supongamos que tenemos un triángulo rectángulo con un ángulo de 30 grados y una hipotenusa de 10 cm. ¿Cuál es la altura del triángulo?

altura = seno (30) * 10
altura = 5 cm

Por lo tanto, la altura del triángulo es de 5 cm.

Conclusión

La altura es un concepto matemático fundamental que se utiliza en muchas áreas, desde la geometría hasta la trigonometría. En geometría, la altura se refiere a la línea perpendicular que se dibuja desde un vértice de un triángulo a su base, mientras que en trigonometría, la altura se refiere a la altura de un triángulo rectángulo o de un objeto medido desde el nivel del suelo. Con las fórmulas y ejemplos proporcionados en este artículo, esperamos que hayas adquirido una comprensión sólida del concepto de altura y cómo se puede calcular en diferentes situaciones.

Preguntas frecuentes

¿Qué es la altura en matemáticas?

La altura es un concepto matemático fundamental que se utiliza en muchas áreas, desde la geometría hasta la trigonometría. En términos simples, la altura se define como la distancia vertical entre un punto y una línea base.

¿Cómo se calcula la altura en un triángulo?

La fórmula para encontrar la altura de un triángulo es la siguiente: altura = (2 * área) / base. Donde el área es la mitad del producto de la base y la altura, y la base es la longitud de la línea que se dibuja desde un extremo del triángulo hasta el otro extremo que es perpendicular a la altura.

¿Cómo se calcula la altura en un rectángulo?

La fórmula para encontrar la altura de un rectángulo es la siguiente: altura = área / base. Donde el área es el producto de la base y la altura del rectángulo.

¿Cómo se calcula la altura en un prisma?

La fórmula para encontrar la altura de un prisma es la siguiente: altura = volumen / área de la base. Donde el volumen es el producto del área de la base y la altura del prisma, y el área de la base es el área de la forma que se encuentra en la parte inferior del prisma.

¿Cómo se calcula la altura en la trigonometría?

La fórmula para encontrar la altura de un triángulo rectángulo es la siguiente: altura = seno (ángulo) * hipotenusa. Donde el seno del ángulo es la relación entre el lado opuesto al ángulo y la hipotenusa. La hipotenusa