La lógica proposicional: su uso en diversas áreas
En el mundo de la filosofía, la lógica proposicional es una herramienta fundamental para la comprensión de la verdad y la validez de los argumentos. Sin embargo, su uso no se limita únicamente a esta área, sino que se extiende a diversas disciplinas, desde la informática hasta las matemáticas y la física.
¿Qué es la lógica proposicional?
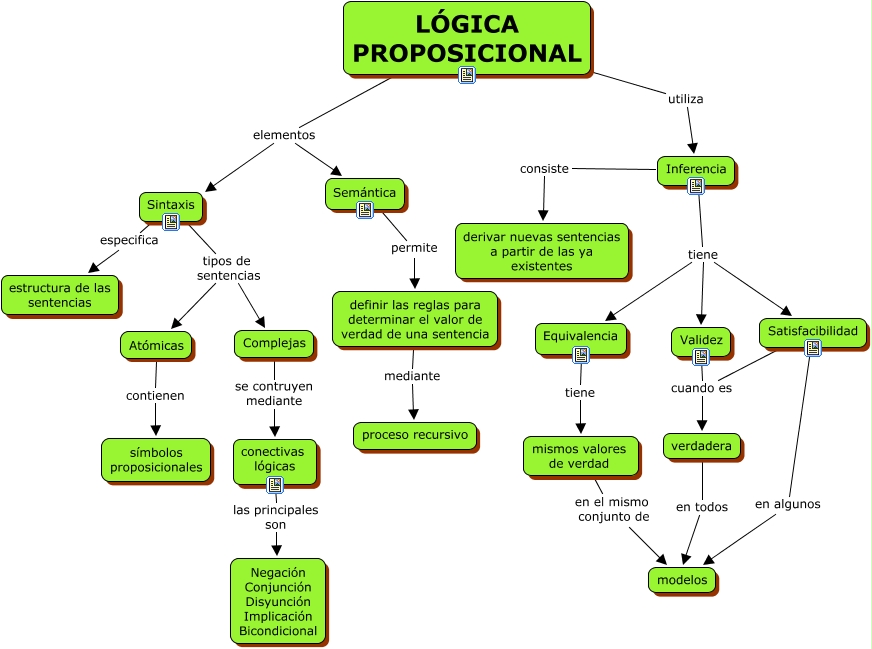
La lógica proposicional es una rama de la lógica que se enfoca en el estudio de las proposiciones, es decir, enunciados que pueden ser verdaderos o falsos. Estas proposiciones se representan mediante símbolos, como "p", "q" o "r", y se combinan mediante conectivas lógicas, como "y", "o" o "no", para formar nuevas proposiciones.
La lógica proposicional en la filosofía
En la filosofía, la lógica proposicional se utiliza para analizar la validez de los argumentos y la estructura de las proposiciones. Por ejemplo, se pueden utilizar tablas de verdad para determinar si un argumento es válido o no, o para identificar las contradicciones en una serie de enunciados.
Además, la lógica proposicional es una herramienta útil para la construcción de argumentos sólidos y coherentes. Al utilizar las conectivas lógicas adecuadas, se pueden establecer relaciones precisas entre las proposiciones, lo que permite construir argumentos más efectivos.
La lógica proposicional en la informática
En la informática, la lógica proposicional se utiliza para la programación y el diseño de sistemas. Los lenguajes de programación, por ejemplo, se basan en la lógica proposicional para la construcción de algoritmos y la resolución de problemas.
En el diseño de sistemas, la lógica proposicional se utiliza para la creación de circuitos lógicos y la optimización de su funcionamiento. Los circuitos lógicos se construyen utilizando puertas lógicas, que representan las conectivas lógicas de la lógica proposicional.
La lógica proposicional en las matemáticas
En las matemáticas, la lógica proposicional se utiliza para la demostración de teoremas y la construcción de modelos matemáticos. Por ejemplo, en la teoría de conjuntos, se utiliza la lógica proposicional para definir las operaciones de unión, intersección y complemento.
Además, la lógica proposicional es una herramienta fundamental para la lógica matemática, que se enfoca en el estudio de la verdad y la deducción en las matemáticas. La lógica proposicional se utiliza para la construcción de sistemas formales, como la lógica de primer orden, que permiten la demostración rigurosa de teoremas matemáticos.
La lógica proposicional en la física
En la física, la lógica proposicional se utiliza para la formulación de teorías y la resolución de problemas. Por ejemplo, en la mecánica clásica, se utilizan las leyes de la lógica proposicional para la formulación de ecuaciones y la resolución de problemas de movimiento.
En la física moderna, la lógica proposicional se utiliza para la formulación de teorías cuánticas, que describen el comportamiento de las partículas subatómicas. La lógica proposicional se utiliza para la identificación de relaciones entre proposiciones, lo que permite la construcción de modelos matemáticos precisos.
Conclusión
La lógica proposicional es una herramienta fundamental en diversas áreas del conocimiento, desde la filosofía hasta la física. Su capacidad para la construcción de argumentos sólidos y la identificación de relaciones precisas entre proposiciones la convierten en una herramienta valiosa para la resolución de problemas y la formulación de teorías.
Preguntas frecuentes
1. ¿Qué es una proposición?
Una proposición es un enunciado que puede ser verdadero o falso.
2. ¿Qué son las conectivas lógicas?
Las conectivas lógicas son símbolos que se utilizan para combinar proposiciones y formar nuevas proposiciones. Algunas de las conectivas lógicas más comunes son "y", "o" y "no".
3. ¿Cómo se utiliza la lógica proposicional en la programación?
En la programación, la lógica proposicional se utiliza para la construcción de algoritmos y la resolución de problemas. Los lenguajes de programación se basan en la lógica proposicional para la construcción de programas y la optimización de su funcionamiento.
4. ¿Qué es la lógica matemática?
La lógica matemática es una rama de la lógica que se enfoca en el estudio de la verdad y la deducción en las matemáticas. La lógica proposicional es una herramienta fundamental para la construcción de sistemas formales, como la lógica de primer orden, que permiten la demostración rigurosa de teoremas matemáticos.
5. ¿Cómo se utiliza la lógica proposicional en la física moderna?
En la física moderna, la lógica proposicional se utiliza para la formulación de teorías cuánticas, que describen el comportamiento de las partículas subatómicas. La lógica proposicional se utiliza para la identificación de relaciones entre proposiciones, lo que permite la construcción de modelos matemáticos precisos.
Deja una respuesta