La relación entre principio de buena ordenación y axioma de elección

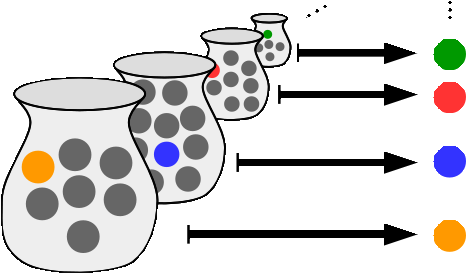
En el mundo de las matemáticas existe una relación interesante entre el principio de buena ordenación y el axioma de elección. Ambos conceptos son fundamentales en la teoría de conjuntos y se utilizan para establecer diversas propiedades de los conjuntos. En este artículo, profundizaremos en esta relación y explicaremos cómo se utilizan estos principios en las matemáticas.

¿Qué es el principio de buena ordenación?

El principio de buena ordenación (PBO) es un principio matemático que establece que todo conjunto no vacío puede ser bien ordenado. La buena ordenación es un tipo de ordenamiento que se utiliza para establecer un orden dentro de un conjunto. En un conjunto bien ordenado, cada subconjunto no vacío tiene un elemento mínimo.

Por ejemplo, considere el conjunto de números naturales {1, 2, 3, …}. Este conjunto puede ser bien ordenado utilizando el orden natural de los números. En este caso, el elemento mínimo del conjunto es 1. El principio de buena ordenación es importante porque nos permite establecer propiedades de los conjuntos bien ordenados y utilizarlas en la teoría de conjuntos.

¿Qué es el axioma de elección?

El axioma de elección (AE) es otro principio matemático que establece que, dada una colección de conjuntos no vacíos, es posible elegir un elemento de cada conjunto. En otras palabras, el axioma de elección nos permite construir un conjunto que contenga un elemento de cada uno de los conjuntos de una colección.

Por ejemplo, considere la colección de conjuntos A = {{1, 2}, {3, 4}, {5, 6}}. El axioma de elección nos permite construir un conjunto que contenga un elemento de cada uno de los conjuntos de A. En este caso, podríamos construir el conjunto {1, 3, 5}.

El axioma de elección es importante en la teoría de conjuntos porque nos permite establecer propiedades de los conjuntos que no son bien ordenados. Esto es especialmente útil en la teoría de conjuntos infinitos, donde los conjuntos no pueden ser bien ordenados.

La relación entre PBO y AE

La relación entre el principio de buena ordenación y el axioma de elección es interesante porque ambos principios se utilizan para establecer propiedades de los conjuntos en la teoría de conjuntos. En particular, el axioma de elección implica el principio de buena ordenación.

Para entender esta relación, consideremos el siguiente argumento. Suponga que tenemos un conjunto X que no es bien ordenado. En este caso, podemos construir una colección de subconjuntos de X que no tienen elementos mínimos. Para hacer esto, tomamos un elemento de X y lo eliminamos del conjunto. Luego, tomamos otro elemento de X que es menor que el primero y lo eliminamos del conjunto. Continuamos de esta manera hasta que no queden elementos en X.

Ahora, supongamos que aplicamos el axioma de elección a esta colección de subconjuntos de X. Esto nos permite construir un conjunto que contenga un elemento de cada uno de los subconjuntos. Sin embargo, este conjunto no puede ser bien ordenado, ya que contiene elementos que no tienen un elemento mínimo. Por lo tanto, el axioma de elección implica que el principio de buena ordenación es verdadero.

Aplicaciones de PBO y AE

El principio de buena ordenación y el axioma de elección tienen muchas aplicaciones en las matemáticas. Por ejemplo, se utilizan para establecer la existencia de bases de espacios vectoriales y para demostrar el teorema de Zorn, que establece que todo conjunto parcialmente ordenado tiene un elemento maximal.

Además, estos principios se utilizan en la teoría de conjuntos para establecer la existencia de ciertos conjuntos que no pueden ser construidos utilizando otros principios. Por ejemplo, el axioma de elección se utiliza para demostrar la existencia de números cardinales y ordinales, que son fundamentales en la teoría de conjuntos.

Preguntas frecuentes

¿Qué es un conjunto bien ordenado?

Un conjunto bien ordenado es un conjunto en el que cada subconjunto no vacío tiene un elemento mínimo. Por ejemplo, el conjunto de números naturales {1, 2, 3, …} es bien ordenado utilizando el orden natural de los números.

¿Por qué es importante el principio de buena ordenación?

El principio de buena ordenación es importante porque nos permite establecer propiedades de los conjuntos bien ordenados y utilizarlas en la teoría de conjuntos.

¿Qué es el axioma de elección?

El axioma de elección es un principio matemático que establece que, dada una colección de conjuntos no vacíos, es posible elegir un elemento de cada conjunto.

¿Por qué es importante el axioma de elección?

El axioma de elección es importante en la teoría de conjuntos porque nos permite establecer propiedades de los conjuntos que no son bien ordenados. Esto es especialmente útil en la teoría de conjuntos infinitos, donde los conjuntos no pueden ser bien ordenados.

¿Cómo se utilizan el principio de buena ordenación y el axioma de elección en las matemáticas?

El principio de buena ordenación y el axioma de elección se utilizan en las matemáticas para establecer propiedades de los conjuntos y para demostrar la existencia de ciertos conjuntos que no pueden ser construidos utilizando otros principios. También se utilizan para establecer la existencia de bases de espacios vectoriales y para demostrar el teorema de Zorn.