Tautología vs. Contradicción: ¿Cómo diferenciarlas? Ejemplos claros
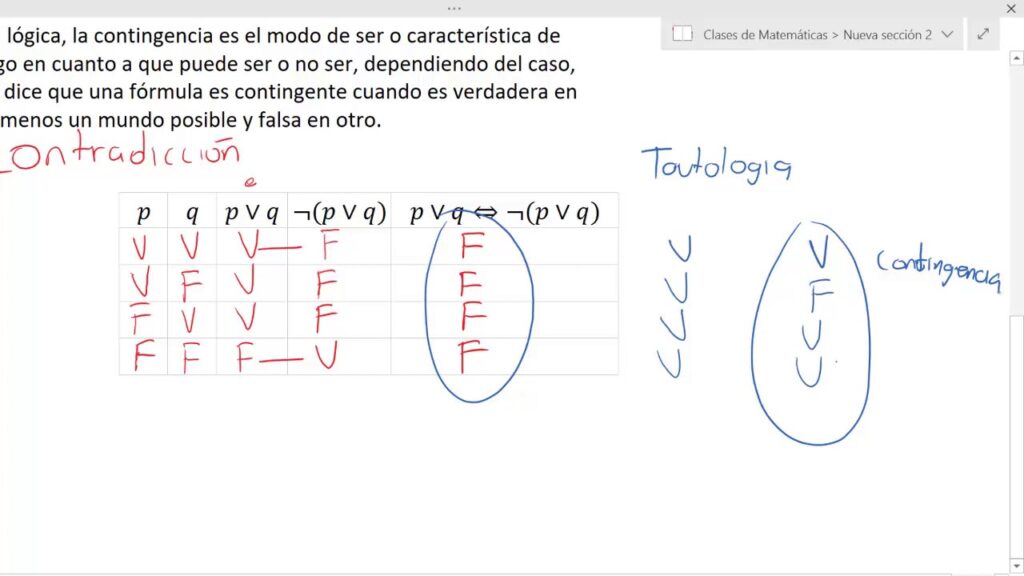
Cuando se trata de lógica y argumentación, es importante entender la diferencia entre una tautología y una contradicción. Ambos términos se refieren a declaraciones que son verdaderas o falsas de manera absoluta, pero hay una gran diferencia entre ellas.
- ¿Qué es una tautología?
- ¿Qué es una contradicción?
- ¿Cómo diferenciar una tautología de una contradicción?
- Ejemplos de tautologías y contradicciones
- Conclusión
-
Preguntas frecuentes
- 1. ¿Por qué es importante diferenciar entre una tautología y una contradicción?
- 2. ¿Puede una declaración ser ambas, una tautología y una contradicción?
- 3. ¿Puede una declaración ser ni una tautología ni una contradicción?
- 4. ¿Por qué las tautologías son importantes en matemáticas y lógica?
- 5. ¿Por qué las contradicciones son problemáticas en la argumentación?
¿Qué es una tautología?
Una tautología es una declaración que es verdadera en todas las situaciones. En otras palabras, no hay ninguna situación en la que la declaración sea falsa. Por ejemplo, la declaración "El sol es el sol" es una tautología. Es obvio que el sol es el sol, y no hay ningún caso en el que esto no sea cierto.
Otro ejemplo de tautología es la siguiente declaración: "Todos los solteros están solteros". Esta afirmación es verdadera por definición, ya que la palabra "soltero" se refiere a alguien que no está casado. Por lo tanto, es imposible que un soltero no esté soltero.
¿Qué es una contradicción?
Una contradicción, por otro lado, es una declaración que es falsa en todas las situaciones. En otras palabras, no hay ninguna situación en la que la declaración sea verdadera. Por ejemplo, la declaración "El sol es la luna" es una contradicción. Es imposible que el sol sea la luna, y siempre será falso.
Otro ejemplo de contradicción es la siguiente declaración: "Este círculo es un cuadrado". Esto es falso por definición, ya que un círculo y un cuadrado son formas geométricas diferentes. No hay ninguna situación en la que sea posible que un círculo sea un cuadrado.
¿Cómo diferenciar una tautología de una contradicción?
La principal diferencia entre una tautología y una contradicción es que una tautología es una afirmación verdadera en todas las situaciones, mientras que una contradicción es falsa en todas las situaciones.
Para determinar si una declaración es una tautología o una contradicción, debemos examinar su contenido y contexto. Si la declaración es verdadera por definición, entonces es una tautología. Si la declaración es falsa por definición, entonces es una contradicción.
Por ejemplo, la declaración "Los seres humanos necesitan aire para respirar" es una tautología, ya que es cierto por definición que los seres humanos necesitan aire para respirar. Por otro lado, la declaración "Los pájaros pueden volar bajo el agua" es una contradicción, ya que es falso por definición que los pájaros puedan volar bajo el agua.
Ejemplos de tautologías y contradicciones
A continuación, se presentan algunos ejemplos de tautologías y contradicciones para ayudar a comprender mejor la diferencia entre estos dos términos:
Tautologías:
- La nieve es blanca.
- Los padres son mayores que sus hijos.
- Los triángulos tienen tres lados.
- 1+1=2.
Contradicciones:
- Los círculos tienen ángulos rectos.
- Los perros son felinos.
- La lluvia es seca.
- 2+2=5.
Conclusión
Las tautologías y las contradicciones son declaraciones que son verdaderas o falsas de manera absoluta. Las tautologías son verdaderas en todas las situaciones, mientras que las contradicciones son falsas en todas las situaciones. Para determinar si una declaración es una tautología o una contradicción, debemos examinar su contenido y contexto.
Preguntas frecuentes
1. ¿Por qué es importante diferenciar entre una tautología y una contradicción?
Es importante diferenciar entre una tautología y una contradicción porque nos ayuda a evaluar la validez de los argumentos y las proposiciones. Si una declaración es una tautología o una contradicción, entonces no aporta ningún valor informativo al argumento.
2. ¿Puede una declaración ser ambas, una tautología y una contradicción?
No, una declaración no puede ser ambas, una tautología y una contradicción. Una tautología es verdadera en todas las situaciones, mientras que una contradicción es falsa en todas las situaciones. Por lo tanto, una declaración no puede ser verdadera y falsa al mismo tiempo.
3. ¿Puede una declaración ser ni una tautología ni una contradicción?
Sí, una declaración puede ser ni una tautología ni una contradicción. Existen declaraciones que son verdaderas en algunas situaciones y falsas en otras situaciones. Estas declaraciones son llamadas contingentes.
4. ¿Por qué las tautologías son importantes en matemáticas y lógica?
Las tautologías son importantes en matemáticas y lógica porque son la base de muchas demostraciones y teoremas. Las tautologías son verdaderas por definición, lo que significa que podemos utilizarlas como premisas para construir argumentos válidos.
5. ¿Por qué las contradicciones son problemáticas en la argumentación?
Las contradicciones son problemáticas en la argumentación porque invalidan todo el argumento. Si una premisa es una contradicción, entonces el argumento no puede ser válido, ya que una contradicción es falsa en todas las situaciones.
Deja una respuesta