Comparación de razones: aprende a resolver casos simples en 6to grado

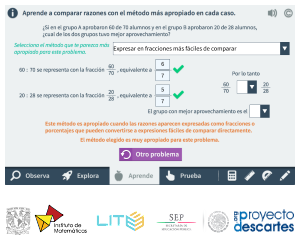
En el sexto grado, los estudiantes comienzan a aprender sobre la comparación de razones. Las razones son la relación entre dos cantidades y se expresan como una fracción. La comparación de razones implica comparar dos relaciones diferentes y determinar cuál es mayor o menor. Este concepto es importante para la resolución de problemas matemáticos y para la vida cotidiana en general. En este artículo, explicaremos cómo resolver casos simples de comparación de razones en el sexto grado.

¿Qué es una razón?

Una razón es la relación entre dos cantidades. Por ejemplo, si tenemos 6 manzanas y 3 naranjas, la razón de manzanas a naranjas es 6:3 o 2:1. La razón se puede expresar como una fracción, en este caso, 2/1. La fracción indica cuántas veces es mayor la cantidad de manzanas en comparación con las naranjas.

Comparación de razones

La comparación de razones implica comparar dos relaciones diferentes. Por ejemplo, si tenemos 6 manzanas y 3 naranjas en una canasta y 4 manzanas y 2 naranjas en otra canasta, podemos comparar las razones de manzanas a naranjas de ambas canastas para determinar cuál canasta tiene más manzanas en relación con las naranjas. La razón de la primera canasta es 6:3 o 2:1, mientras que la razón de la segunda canasta es 4:2 o 2:1. Ambas razones son iguales, lo que significa que ambas canastas tienen la misma relación de manzanas a naranjas.

Resolución de problemas de comparación de razones

Para resolver problemas de comparación de razones, es importante identificar las dos relaciones que estamos comparando. Luego, podemos expresar ambas relaciones como fracciones y compararlas. Si las fracciones son iguales, las dos relaciones son equivalentes. Si una fracción es mayor que la otra, entonces la relación correspondiente tiene más de una cantidad en comparación con la otra relación.

Ejemplo 1:

En una carrera de 100 metros, Juan corrió la distancia en 10 segundos, mientras que Pedro corrió la distancia en 12 segundos. ¿Quién corrió más rápido?
- La razón de la velocidad de Juan es de 100:10 o 10:1.
- La razón de la velocidad de Pedro es de 100:12 o 25:3.
- Podemos comparar ambas razones expresadas como fracciones: 10/1 y 25/3.
- Para comparar fracciones, necesitamos tener un denominador común. Podemos convertir 10/1 en 30/3.
- Ahora podemos comparar ambas fracciones: 30/3 es mayor que 25/3.
- Por lo tanto, la razón de la velocidad de Juan es mayor que la razón de la velocidad de Pedro, lo que significa que Juan corrió más rápido.

Ejemplo 2:

En un grupo de estudiantes, hay 20 niñas y 30 niños. ¿Cuál es la razón de niñas a niños? ¿Y cuál es la razón de niños a niñas?
- La razón de niñas a niños es de 20:30 o 2:3.
- La razón de niños a niñas es de 30:20 o 3:2.
- Podemos ver que ambas razones son diferentes. La razón de niños a niñas es mayor que la razón de niñas a niños.
- Esto significa que hay más niños que niñas en el grupo.

Conclusión

La comparación de razones es una habilidad matemática importante que se aprende en el sexto grado. A través de la comparación de fracciones, se pueden determinar relaciones equivalentes y cuál relación tiene más de una cantidad en comparación con otra. Esta habilidad es importante para la resolución de problemas matemáticos y para la vida cotidiana en general.

Preguntas frecuentes

1. ¿Cuál es la fórmula para calcular la razón?

La razón se expresa como una fracción, por lo que no hay una fórmula específica para calcularla. Simplemente se divide una cantidad por otra y se expresa como una fracción.

2. ¿La razón siempre tiene que ser expresada como una fracción?

Sí, la razón siempre se expresa como una fracción. Esto es porque la razón es una relación entre dos cantidades y se necesita una fracción para mostrar esta relación.

3. ¿Cómo se comparan las fracciones?

Para comparar fracciones, es importante tener un denominador común. Si las fracciones tienen diferentes denominadores, se pueden convertir a un denominador común antes de compararlas.

4. ¿Qué tan importante es la comparación de razones en la vida cotidiana?

La comparación de razones es importante en la vida cotidiana para determinar cuántas veces es mayor una cantidad en comparación con otra cantidad. Por ejemplo, al comprar productos en una tienda, se pueden comparar los precios por unidad para determinar cuál es más económico.

5. ¿Cuáles son algunas aplicaciones de la comparación de razones en el mundo real?

La comparación de razones se utiliza en una variedad de campos, como la economía, la ingeniería y la estadística. Por ejemplo, en la economía, se pueden comparar las razones de ingresos a gastos para determinar la rentabilidad de un negocio. En la ingeniería, se pueden comparar las razones de fuerza a peso para determinar la eficiencia de un diseño. Y en la estadística, se pueden comparar las razones de diferentes grupos para identificar patrones y tendencias.