Descubre la lógica tradicional en la filosofía: conceptos clave

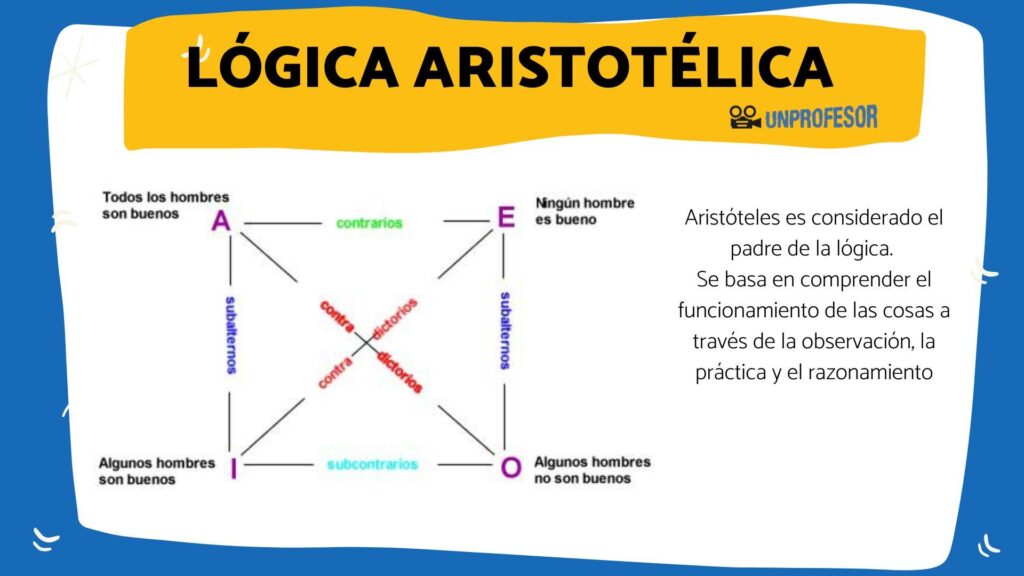
La lógica tradicional es una rama de la filosofía que se ha ocupado de estudiar el razonamiento humano. En ella, se han desarrollado diversos conceptos clave que nos permiten entender cómo funciona nuestro pensamiento y cómo podemos distinguir entre argumentos válidos e inválidos. En este artículo, vamos a descubrir algunos de estos conceptos clave y su importancia en la lógica tradicional.

Concepto de proposición

Una proposición es una afirmación que puede ser verdadera o falsa. Por ejemplo, "el cielo es azul" es una proposición que puede ser verdadera o falsa dependiendo de las circunstancias. En la lógica tradicional, las proposiciones son la materia prima del razonamiento. Los argumentos están formados por proposiciones que se relacionan entre sí, y la validez de un argumento depende de la relación lógica entre sus proposiciones.

Concepto de premisa

Una premisa es una proposición que se utiliza para respaldar una conclusión. En un argumento, las premisas son las afirmaciones que se utilizan para llegar a una conclusión. Por ejemplo, en el argumento "todos los hombres son mortales; Sócrates es un hombre; por lo tanto, Sócrates es mortal", las dos primeras afirmaciones son las premisas, mientras que la última es la conclusión.

Concepto de conclusión

La conclusión es la proposición a la que se llega a través de un argumento. En un argumento válido, la conclusión sigue necesariamente de las premisas. Por ejemplo, en el argumento anterior, la conclusión "Sócrates es mortal" sigue necesariamente de las premisas "todos los hombres son mortales" y "Sócrates es un hombre".

Concepto de argumento válido

Un argumento es válido si su conclusión sigue necesariamente de sus premisas. Es decir, si las premisas son verdaderas, entonces la conclusión también debe serlo. Por ejemplo, el argumento anterior es válido porque la conclusión "Sócrates es mortal" sigue necesariamente de las premisas "todos los hombres son mortales" y "Sócrates es un hombre".

Concepto de argumento sólido

Un argumento es sólido si es válido y todas sus premisas son verdaderas. Por ejemplo, el argumento "todos los hombres son mortales; Sócrates es un hombre; por lo tanto, Sócrates es mortal" es sólido porque es válido y todas sus premisas son verdaderas.

Concepto de silogismo

Un silogismo es un tipo de argumento que consta de tres proposiciones: dos premisas y una conclusión. En un silogismo, la conclusión sigue necesariamente de las dos premisas. Por ejemplo, "todos los hombres son mortales; Sócrates es un hombre; por lo tanto, Sócrates es mortal" es un silogismo.

Concepto de falacia

Una falacia es un error en el razonamiento que hace que un argumento sea inválido o poco convincente. Hay muchas falacias diferentes, como la falacia ad hominem, la falacia del hombre de paja y la falacia del falso dilema. Es importante identificar las falacias en los argumentos para poder evaluar su validez.

Concepto de proposición compuesta

Una proposición compuesta es una proposición que está formada por dos o más proposiciones simples. Por ejemplo, "Juan estudia y María trabaja" es una proposición compuesta que está formada por las proposiciones simples "Juan estudia" y "María trabaja". Las proposiciones compuestas son importantes en la lógica tradicional porque permiten construir argumentos más complejos.

Concepto de conectivos lógicos

Los conectivos lógicos son palabras o símbolos que se utilizan para combinar proposiciones simples en proposiciones compuestas. Algunos ejemplos de conectivos lógicos son "y", "o" y "si... entonces". Los conectivos lógicos son importantes en la lógica tradicional porque nos permiten construir proposiciones compuestas más complejas y evaluar su validez.

Concepto de negación

La negación es un tipo de conectivo lógico que se utiliza para formar la negación de una proposición. Por ejemplo, la negación de la proposición "el cielo es azul" es "el cielo no es azul". La negación es importante en la lógica tradicional porque nos permite construir proposiciones compuestas más complejas y evaluar su validez.

Concepto de inferencia

La inferencia es el proceso mental que nos permite llegar a una conclusión a partir de unas premisas. En la lógica tradicional, la inferencia es esencial para construir argumentos válidos y sólidos.

Concepto de reglas de inferencia

Las reglas de inferencia son reglas que nos permiten pasar de unas premisas a una conclusión de forma válida. Por ejemplo, la regla de inferencia modus ponens nos permite inferir una conclusión a partir de una premisa y una proposición que afirma la implicación de la premisa con la conclusión. Las reglas de inferencia son importantes en la lógica tradicional porque nos permiten evaluar la validez de los argumentos.

Concepto de demostración

Una demostración es un argumento que muestra que una proposición es verdadera. En la lógica tradicional, las demostraciones son esenciales para establecer la verdad de las proposiciones y construir conocimiento.

Concepto de axioma

Un axioma es una proposición que se acepta como verdadera sin necesidad de demostración. Los axiomas son esenciales en la lógica tradicional porque nos permiten establecer las bases para construir otros conocimientos.

Concepto de teorema

Un teorema es una proposición que se demuestra a partir de otras proposiciones. En la lógica tradicional, los teoremas son importantes porque nos permiten construir conocimientos a partir de otros conocimientos previamente establecidos.

Conclusión

La lógica tradicional es una rama de la filosofía que se ha ocupado de estudiar el razonamiento humano. En ella, se han desarrollado diversos conceptos clave que nos permiten entender cómo funciona nuestro pensamiento y cómo podemos distinguir entre argumentos válidos e inválidos. Los conceptos de proposición, premisa, conclusión, argumento válido, argumento sólido, silogismo, falacia, proposición compuesta, conectivos lógicos, negación, inferencia, reglas de inferencia, demostración, axioma y teorema son esenciales en la lógica tradicional y nos permiten construir conocimiento y evaluar la validez de los argumentos.

Preguntas frecuentes

¿Por qué es importante la lógica tradicional?

La lógica tradicional es importante porque nos permite entender cómo funciona nuestro pensamiento y cómo podemos distinguir entre argumentos válidos e inválidos. Además, nos permite construir conocimiento a partir de otros conocimientos previamente establec