Cuadro sinóptico de lógica matemática: todo lo que necesitas saber

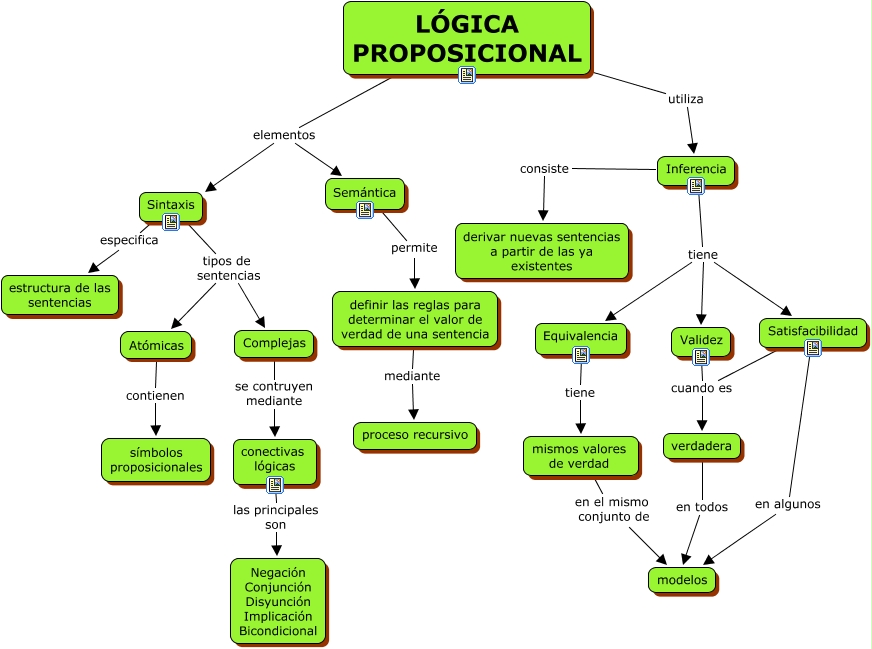
La lógica matemática es una rama de las matemáticas que se enfoca en el estudio de la validez de los argumentos. En otras palabras, se trata de un conjunto de herramientas que nos permiten analizar la coherencia y la consistencia de los razonamientos. Si estás interesado en aprender más sobre lógica matemática, has llegado al lugar indicado. En este artículo, te presentaremos un cuadro sinóptico que resume todo lo que necesitas saber sobre este tema.

¿Qué es la lógica matemática?

La lógica matemática es una disciplina que se encarga de estudiar los principios y técnicas que se utilizan para analizar la validez de los argumentos. En otras palabras, se trata de un conjunto de herramientas que nos permiten determinar si un razonamiento es correcto o no.

¿Cuáles son los principales conceptos de la lógica matemática?

Los principales conceptos de la lógica matemática son:

• Proposición: una unidad de significado que puede ser verdadera o falsa.
• Conectores lógicos: herramientas que nos permiten combinar proposiciones para construir argumentos más complejos.
• Tablas de verdad: herramientas que nos permiten determinar la verdad o falsedad de una proposición o de un conjunto de proposiciones.
• Argumentos: una secuencia de proposiciones que tienen como objetivo demostrar una conclusión.
• Reglas de inferencia: herramientas que nos permiten derivar conclusiones a partir de premisas.

¿Cuáles son los principales conectores lógicos?

Los principales conectores lógicos son:

• Negación: se utiliza para construir la proposición contraria a otra proposición.
• Conjunción: se utiliza para combinar dos proposiciones con el objetivo de construir una proposición compuesta que sea verdadera sólo si ambas proposiciones son verdaderas.
• Disyunción: se utiliza para combinar dos proposiciones con el objetivo de construir una proposición compuesta que sea verdadera si al menos una de las proposiciones es verdadera.
• Condicional: se utiliza para construir una proposición que establece una relación de implicación entre dos proposiciones. La proposición compuesta es verdadera si la proposición antecedente es verdadera y la proposición consecuente es verdadera o falsa.
• Bicondicional: se utiliza para construir una proposición que establece una relación de equivalencia entre dos proposiciones. La proposición compuesta es verdadera si ambas proposiciones tienen el mismo valor de verdad.

¿Qué son las tablas de verdad?

Las tablas de verdad son herramientas que nos permiten determinar la verdad o falsedad de una proposición o de un conjunto de proposiciones. Las tablas de verdad son muy útiles para analizar la validez de los argumentos y para demostrar que una proposición es una tautología, una contradicción o contingente.

¿Cómo se construyen los argumentos en lógica matemática?

Para construir un argumento en lógica matemática, es necesario seguir los siguientes pasos:

1. Identificar las premisas y la conclusión del argumento.
2. Analizar las premisas para determinar si son verdaderas o falsas.
3. Utilizar las reglas de inferencia para derivar la conclusión a partir de las premisas.
4. Evaluar la validez del argumento.

¿Cuáles son las principales reglas de inferencia?

Las principales reglas de inferencia son:

• Modus ponens: si A implica B y A es verdadera, entonces B es verdadera.
• Modus tollens: si A implica B y B es falsa, entonces A es falsa.
• Silogismo hipotético: si A implica B y B implica C, entonces A implica C.
• Silogismo disyuntivo: si A o B es verdadera y A implica C y B implica D, entonces C o D es verdadera.
• Reducción al absurdo: si asumimos que A es verdadera y llegamos a una contradicción, entonces A es falsa.

Conclusión

La lógica matemática es una disciplina muy importante que nos permite analizar la validez de los argumentos y construir razonamientos sólidos y coherentes. En este artículo, te hemos presentado un cuadro sinóptico que resume los principales conceptos de la lógica matemática, incluyendo las proposiciones, los conectores lógicos, las tablas de verdad, los argumentos y las reglas de inferencia. Esperamos que esta información te sea de utilidad y que puedas aplicarla en tus estudios o en tu vida cotidiana.

Preguntas frecuentes

1. ¿Qué es la lógica matemática?

La lógica matemática es una disciplina que se encarga de estudiar los principios y técnicas que se utilizan para analizar la validez de los argumentos.

2. ¿Cuáles son los principales conectores lógicos?

Los principales conectores lógicos son la negación, la conjunción, la disyunción, el condicional y el bicondicional.

3. ¿Qué son las tablas de verdad?

Las tablas de verdad son herramientas que nos permiten determinar la verdad o falsedad de una proposición o de un conjunto de proposiciones.

4. ¿Cómo se construyen los argumentos en lógica matemática?

Para construir un argumento en lógica matemática, es necesario identificar las premisas y la conclusión del argumento, analizar las premisas, utilizar las reglas de inferencia y evaluar la validez del argumento.

5. ¿Cuáles son las principales reglas de inferencia?

Las principales reglas de inferencia son el modus ponens, el modus tollens, el silogismo hipotético, el silogismo disyuntivo y la reducción al absurdo.