Descubre la lógica probabilística: concepto y aplicaciones
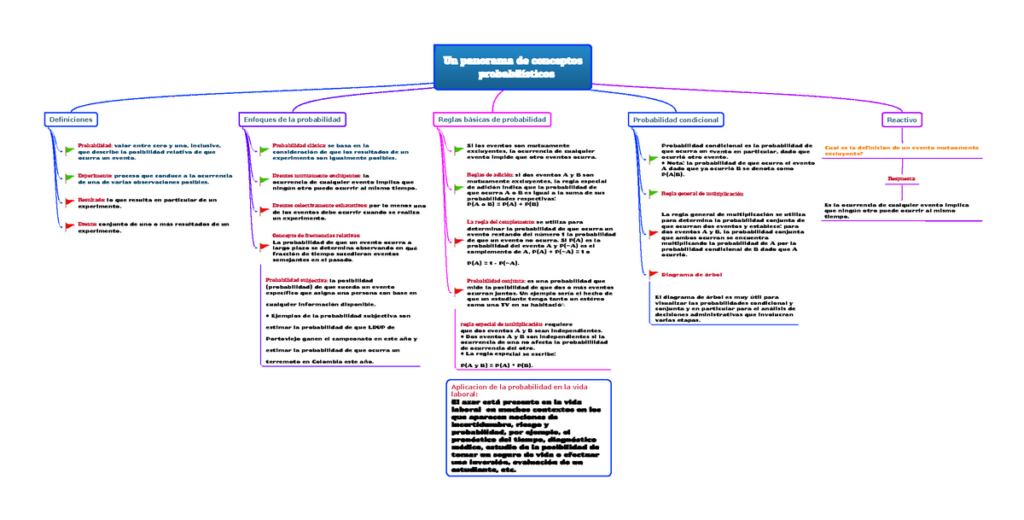
La lógica probabilística es un método matemático que se utiliza para analizar y predecir eventos que tienen cierto grado de incertidumbre. En lugar de basarse en la certeza de una proposición, la lógica probabilística se basa en la probabilidad de que una proposición sea verdadera o falsa.
La lógica probabilística es una herramienta esencial en la estadística, la inteligencia artificial y muchas otras áreas de la ciencia. En este artículo, exploraremos el concepto de la lógica probabilística y sus aplicaciones en el mundo real.
¿Qué es la lógica probabilística?
La lógica probabilística es una extensión de la lógica clásica que permite trabajar con proposiciones que tienen un grado de incertidumbre. En lugar de afirmar categóricamente que una proposición es verdadera o falsa, la lógica probabilística asigna una probabilidad a cada proposición.
La probabilidad es una medida de la certeza o incertidumbre de una proposición. La probabilidad de una proposición puede ser expresada como un número entre 0 y 1, donde 0 significa que la proposición es falsa con certeza absoluta, y 1 significa que la proposición es verdadera con certeza absoluta.
La lógica probabilística utiliza reglas matemáticas para combinar las probabilidades de varias proposiciones y generar nuevas probabilidades. Estas reglas se basan en el teorema de Bayes, que establece cómo se deben actualizar las probabilidades cuando se tienen nuevas evidencias.
Aplicaciones de la lógica probabilística
La lógica probabilística tiene una amplia variedad de aplicaciones en el mundo real. Algunas de las más importantes son las siguientes:
Estadística
La lógica probabilística es fundamental en la estadística. La estadística se utiliza para analizar conjuntos de datos y encontrar patrones. La lógica probabilística se utiliza para modelar la incertidumbre en los datos y para hacer predicciones sobre futuros eventos.
Inteligencia artificial
La lógica probabilística es un componente clave de muchos algoritmos de inteligencia artificial. Los algoritmos de aprendizaje automático utilizan la lógica probabilística para aprender a partir de datos y para hacer predicciones sobre nuevos datos.
Medicina
La lógica probabilística se utiliza en medicina para hacer diagnósticos y para diseñar tratamientos. Los médicos utilizan la lógica probabilística para calcular la probabilidad de que un paciente tenga una enfermedad en base a los síntomas y otros factores.
Finanzas
La lógica probabilística se utiliza en finanzas para hacer predicciones sobre el comportamiento del mercado y para evaluar el riesgo de determinados instrumentos financieros. Los inversores utilizan la lógica probabilística para tomar decisiones informadas sobre la inversión de su dinero.
Reglas de la lógica probabilística
La lógica probabilística utiliza varias reglas matemáticas para combinar las probabilidades de varias proposiciones y generar nuevas probabilidades. Las reglas más importantes son las siguientes:
Regla de la suma
La regla de la suma establece que la probabilidad de que suceda A o B es igual a la suma de las probabilidades de A y B, menos la probabilidad de que sucedan ambos al mismo tiempo.
P(A o B) = P(A) + P(B) - P(A y B)
Regla del producto
La regla del producto establece que la probabilidad de que sucedan A y B juntos es igual a la probabilidad de A multiplicada por la probabilidad de B, dada A.
P(A y B) = P(A) * P(B|A)
Teorema de Bayes
El teorema de Bayes es la regla más importante de la lógica probabilística. Establece cómo se deben actualizar las probabilidades cuando se tienen nuevas evidencias.
P(A|B) = P(B|A) * P(A) / P(B)
Donde P(A|B) es la probabilidad de que A sea verdadero dado que B es verdadero, P(B|A) es la probabilidad de que B sea verdadero dado que A es verdadero, P(A) es la probabilidad de que A sea verdadero antes de conocer B, y P(B) es la probabilidad de que B sea verdadero.
Conclusiones
La lógica probabilística es una herramienta esencial en la estadística, la inteligencia artificial, la medicina, las finanzas y muchas otras áreas de la ciencia. La lógica probabilística permite trabajar con proposiciones que tienen un grado de incertidumbre y asignarles probabilidades. Las reglas de la lógica probabilística se basan en el teorema de Bayes y permiten combinar las probabilidades de varias proposiciones y generar nuevas probabilidades.
Preguntas frecuentes
¿Qué es la probabilidad?
La probabilidad es una medida de la certeza o incertidumbre de una proposición. La probabilidad de una proposición puede ser expresada como un número entre 0 y 1, donde 0 significa que la proposición es falsa con certeza absoluta, y 1 significa que la proposición es verdadera con certeza absoluta.
¿Qué es el teorema de Bayes?
El teorema de Bayes establece cómo se deben actualizar las probabilidades cuando se tienen nuevas evidencias. El teorema de Bayes es la regla más importante de la lógica probabilística.
¿Cómo se utiliza la lógica probabilística en la medicina?
La lógica probabilística se utiliza en medicina para hacer diagnósticos y para diseñar tratamientos. Los médicos utilizan la lógica probabilística para calcular la probabilidad de que un paciente tenga una enfermedad en base a los síntomas y otros factores.
¿Cómo se utiliza la lógica probabilística en las finanzas?
La lógica probabilística se utiliza en finanzas para hacer predicciones sobre el comportamiento del mercado y para evaluar el riesgo de determinados instrumentos financieros. Los inversores utilizan la lógica probabilística para tomar decisiones informadas sobre la inversión de su dinero.
¿Qué son las reglas de la lógica probabilística?
Las reglas de la lógica probabilística son reglas matemáticas que se utilizan para combinar las probabilidades de varias proposiciones y generar nuevas probabilidades. Las reglas más importantes son la regla de la suma, la regla del producto y el teorema de Bayes.
Deja una respuesta