Descubre la lógica matemática: conceptos proposicionales
La lógica matemática es una disciplina fascinante que se ocupa del estudio de la inferencia y la demostración. Es una herramienta poderosa para la resolución de problemas en muchas áreas, desde la filosofía hasta la informática y las ciencias naturales. En este artículo, descubrirás los fundamentos de la lógica matemática, en particular los conceptos proposicionales.
¿Qué son las proposiciones?
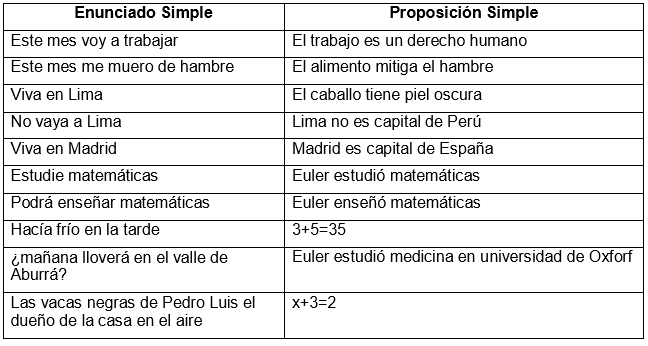
Una proposición es una afirmación que puede ser verdadera o falsa. Por ejemplo, "el cielo es azul" es una proposición que puede ser verdadera o falsa, dependiendo de las circunstancias. "2 + 2 = 5" también es una proposición, pero es falsa. Al contrario, "el sol sale por el oeste" es una proposición que es falsa en cualquier circunstancia.
Conectivos lógicos
Los conectivos lógicos son palabras o símbolos que se utilizan para combinar proposiciones y crear nuevas proposiciones. Los conectivos más comunes son:
- Negación: se representa con el símbolo ¬ y se utiliza para negar una proposición. Por ejemplo, ¬(el cielo es azul) significa "el cielo no es azul".
- Conjunción: se representa con el símbolo ∧ y se utiliza para unir dos proposiciones. Por ejemplo, "el cielo es azul ∧ el sol brilla" significa que ambas proposiciones son verdaderas.
- Disyunción: se representa con el símbolo ∨ y se utiliza para indicar que al menos una de dos proposiciones es verdadera. Por ejemplo, "el cielo es azul ∨ el pasto es verde" significa que al menos una de las dos proposiciones es verdadera.
- Implicación: se representa con el símbolo → y se utiliza para expresar una relación de causa-efecto entre dos proposiciones. Por ejemplo, "si llueve → las calles se mojan" significa que la segunda proposición es verdadera si la primera lo es.
- Doble implicación: se representa con el símbolo ↔ y se utiliza para indicar que dos proposiciones son equivalentes. Por ejemplo, "el cielo es azul ↔ el pasto es verde" significa que ambas proposiciones son verdaderas o ambas son falsas.
Tablas de verdad
Una tabla de verdad es una herramienta útil para analizar la relación entre proposiciones y conectivos lógicos. En una tabla de verdad, se muestran todas las posibles combinaciones de valores de verdad para las proposiciones involucradas y se determina el valor de verdad de la proposición compuesta.
Por ejemplo, si tenemos las proposiciones "el cielo es azul" y "el sol brilla", podemos crear una tabla de verdad para la conjunción de ambas proposiciones:
| El cielo es azul | El sol brilla | El cielo es azul ∧ el sol brilla |
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | F |
En esta tabla, "V" significa verdadero y "F" significa falso. La última columna muestra el valor de verdad de la proposición compuesta "el cielo es azul ∧ el sol brilla" para todas las posibles combinaciones de valores de verdad para las proposiciones individuales.
Leyes lógicas
Las leyes lógicas son reglas que se aplican a las proposiciones y los conectivos lógicos para simplificar o demostrar argumentos. Algunas leyes lógicas comunes son:
- Ley de identidad: una proposición es equivalente a sí misma. Por ejemplo, "el cielo es azul" es equivalente a "el cielo es azul".
- Ley de doble negación: la negación de una proposición negada es equivalente a la proposición original. Por ejemplo, ¬(¬el cielo es azul) es equivalente a "el cielo es azul".
- Ley de De Morgan: la negación de una conjunción es equivalente a la disyunción de las negaciones de las proposiciones involucradas. Por ejemplo, ¬(el cielo es azul ∧ el sol brilla) es equivalente a "(¬el cielo es azul) ∨ (¬el sol brilla)".
- Ley de contraposición: la implicación de una proposición es equivalente a la implicación de su contraposición. Por ejemplo, "si llueve → las calles se mojan" es equivalente a "si las calles no se mojan → no llueve".
Conclusiones
La lógica matemática es una herramienta poderosa para la resolución de problemas en muchas áreas. Los conceptos proposicionales, los conectivos lógicos, las tablas de verdad y las leyes lógicas son los fundamentos de la lógica matemática. Con estas herramientas, podemos analizar y simplificar argumentos, determinar la validez de razonamientos y construir sistemas formales.
Preguntas frecuentes
¿Qué es una proposición?
Una proposición es una afirmación que puede ser verdadera o falsa.
¿Qué son los conectivos lógicos?
Los conectivos lógicos son palabras o símbolos que se utilizan para combinar proposiciones y crear nuevas proposiciones.
¿Qué es una tabla de verdad?
Una tabla de verdad es una herramienta para analizar la relación entre proposiciones y conectivos lógicos.
¿Qué son las leyes lógicas?
Las leyes lógicas son reglas que se aplican a las proposiciones y los conectivos lógicos para simplificar o demostrar argumentos.
¿Por qué es importante la lógica matemática?
La lógica matemática es importante porque nos permite analizar y resolver problemas de manera sistemática y rigurosa, y construir sistemas formales que sean precisos y confiables.
Deja una respuesta