Estrutura lógica: proposiciones y conectivos
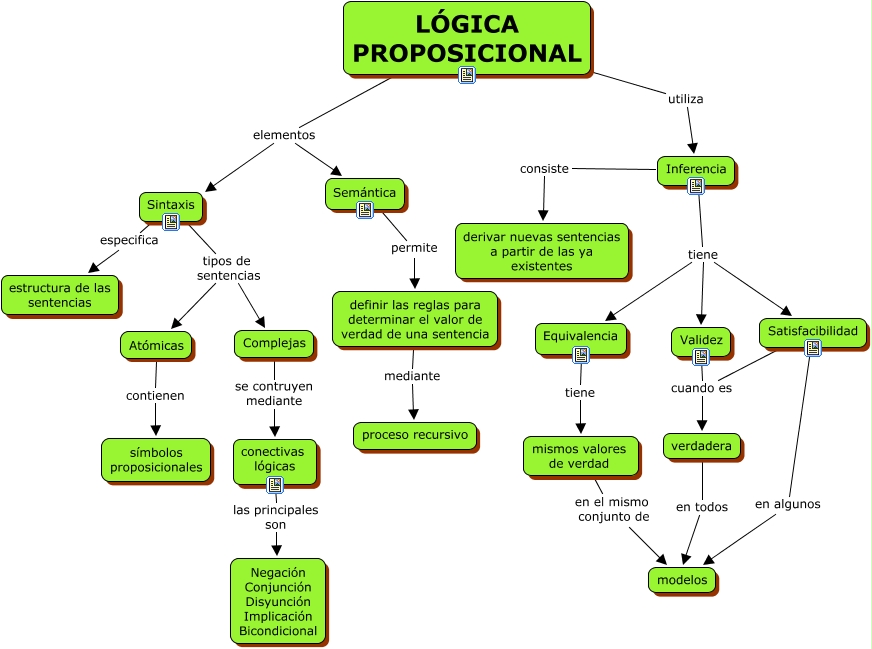
La estructura lógica es una herramienta fundamental para el razonamiento y la argumentación en cualquier ámbito. En este artículo, hablaremos sobre las proposiciones y conectivos, elementos fundamentales de la estructura lógica.
Proposiciones
Una proposición es una afirmación que puede ser verdadera o falsa. Por ejemplo, "El cielo es azul" es una proposición que puede ser verdadera o falsa dependiendo del momento del día y las condiciones atmosféricas. Por otro lado, "El unicornio rosa invisible existe" es una proposición que es falsa.
Es importante destacar que una proposición no es una pregunta ni una orden. Por ejemplo, "¿Estás bien?" no es una proposición, ya que no es una afirmación verdadera o falsa. Asimismo, "¡Cierra la puerta!" no es una proposición, ya que es una orden.
Conectivos
Los conectivos son palabras que permiten combinar proposiciones para formar nuevas proposiciones más complejas. Los conectivos más comunes son:
- Negación: se utiliza para negar una proposición. Se representa con el símbolo ¬. Por ejemplo, si P es la proposición "El cielo es azul", ¬P sería "El cielo no es azul".
- Conjunción: se utiliza para unir dos proposiciones con la condición de que ambas sean verdaderas. Se representa con el símbolo ∧. Por ejemplo, si P es la proposición "El cielo es azul" y Q es la proposición "El sol está brillando", P ∧ Q sería "El cielo es azul y el sol está brillando".
- Disyunción: se utiliza para unir dos proposiciones con la condición de que al menos una sea verdadera. Se representa con el símbolo ∨. Por ejemplo, si P es la proposición "El cielo es azul" y Q es la proposición "Está lloviendo", P ∨ Q sería "El cielo es azul o está lloviendo".
- Implicación: se utiliza para establecer una relación entre dos proposiciones, de tal manera que si la primera es verdadera, entonces la segunda también lo será. Se representa con el símbolo →. Por ejemplo, si P es la proposición "Estudio mucho", y Q es la proposición "Aprobaré el examen", P → Q sería "Si estudio mucho, aprobaré el examen".
- Bicondicional: se utiliza para establecer una relación entre dos proposiciones de tal manera que ambas son verdaderas o ambas son falsas. Se representa con el símbolo ↔. Por ejemplo, si P es la proposición "Estoy viendo televisión", y Q es la proposición "Estoy relajándome", P ↔ Q sería "Estoy viendo televisión si y solo si estoy relajándome".
Tablas de verdad
Una tabla de verdad es una herramienta que permite analizar el valor de verdad de una proposición compleja a partir de las proposiciones más simples que la componen y los conectivos utilizados. Por ejemplo, si queremos analizar la proposición "El cielo es azul y el sol está brillando", podemos hacer la siguiente tabla de verdad:
| P | Q | P ∧ Q |
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | F |
En esta tabla, "V" significa verdadero y "F" significa falso. La columna "P" representa la proposición "El cielo es azul", la columna "Q" representa la proposición "El sol está brillando", y la columna "P ∧ Q" representa la proposición "El cielo es azul y el sol está brillando". Como se puede observar en la tabla, la proposición "El cielo es azul y el sol está brillando" es verdadera solamente cuando ambas proposiciones simples son verdaderas.
Conclusiones
La estructura lógica es fundamental para el razonamiento y la argumentación. Las proposiciones y conectivos son elementos fundamentales de la estructura lógica, y permiten construir proposiciones más complejas a partir de proposiciones simples. Las tablas de verdad son una herramienta útil para analizar el valor de verdad de proposiciones complejas.
Preguntas frecuentes
- ¿Qué es una proposición?
- ¿Qué son los conectivos lógicos?
- ¿Qué es la negación?
- ¿Qué es la implicación?
- ¿Qué son las tablas de verdad?
Una proposición es una afirmación que puede ser verdadera o falsa.
Los conectivos lógicos son palabras que permiten combinar proposiciones para formar nuevas proposiciones más complejas.
La negación es un conectivo que se utiliza para negar una proposición.
La implicación es un conectivo que se utiliza para establecer una relación entre dos proposiciones, de tal manera que si la primera es verdadera, entonces la segunda también lo será.
Las tablas de verdad son una herramienta que permite analizar el valor de verdad de proposiciones complejas a partir de las proposiciones más simples que la componen y los conectivos utilizados.
Deja una respuesta