La Lógica Difusa: Un enfoque innovador en aplicaciones
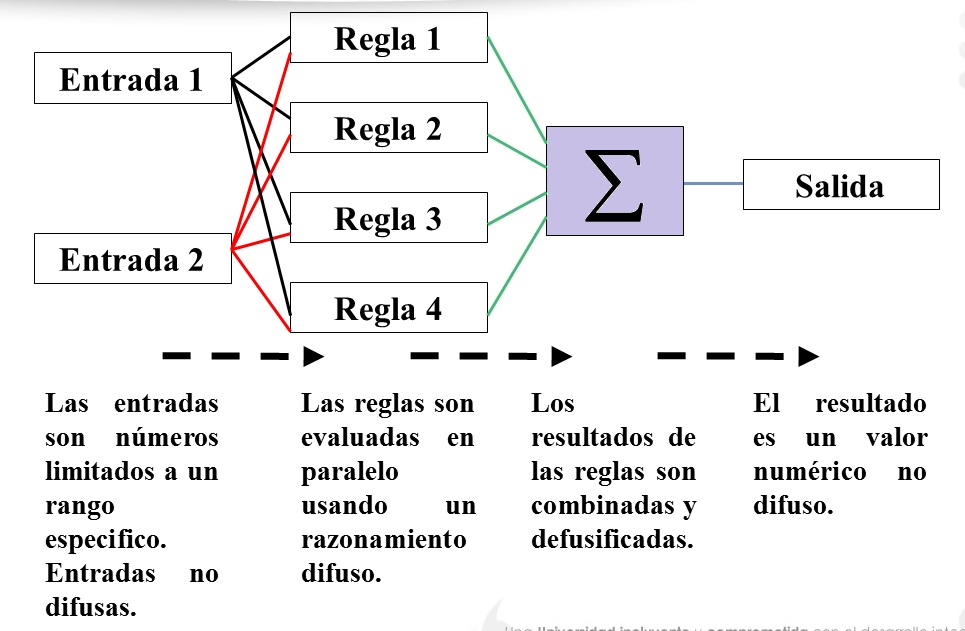
La lógica difusa es un enfoque innovador en la resolución de problemas que permite un razonamiento más cercano al pensamiento humano. A diferencia de la lógica binaria tradicional, que solo permite valores verdaderos o falsos, la lógica difusa permite una escala de valores intermedios que reflejan la incertidumbre del mundo real.
En este artículo, exploraremos las aplicaciones de la lógica difusa en diferentes campos y cómo ha sido utilizada para resolver problemas complejos.
¿Qué es la lógica difusa?
La lógica difusa, también conocida como lógica borrosa, es un enfoque matemático que permite manejar la incertidumbre y la imprecisión en la toma de decisiones. A diferencia de la lógica binaria, que solo permite valores verdaderos o falsos, la lógica difusa permite una escala de valores intermedios.
Esta escala se representa mediante una función de pertenencia, que asigna a cada valor un grado de pertenencia en un conjunto borroso. Por ejemplo, si queremos describir la temperatura de una habitación, podemos utilizar el conjunto borroso "frío", "templado" y "caliente", y asignar a cada valor una función de pertenencia que refleje su grado de pertenencia a cada conjunto.
Aplicaciones de la lógica difusa
La lógica difusa tiene aplicaciones en muchos campos, desde la ingeniería hasta la medicina. Aquí presentamos algunos ejemplos de cómo ha sido utilizada para resolver problemas complejos.
Control de sistemas
La lógica difusa se utiliza en el control de sistemas para manejar la incertidumbre y la imprecisión en la toma de decisiones. Por ejemplo, en el control de un robot, la lógica difusa puede ser utilizada para determinar la velocidad y la dirección del robot en función de las entradas sensoriales y las reglas de control.
Diagnóstico médico
La lógica difusa se utiliza en el diagnóstico médico para manejar la incertidumbre y la imprecisión en la interpretación de los resultados de las pruebas médicas. Por ejemplo, en el diagnóstico de enfermedades cardíacas, la lógica difusa puede ser utilizada para determinar la probabilidad de que un paciente tenga una enfermedad cardíaca en función de los síntomas y los resultados de las pruebas médicas.
Reconocimiento de patrones
La lógica difusa se utiliza en el reconocimiento de patrones para manejar la incertidumbre y la imprecisión en la clasificación de patrones. Por ejemplo, en el reconocimiento de caracteres escritos a mano, la lógica difusa puede ser utilizada para determinar la similitud entre un carácter y una plantilla de referencia en función de sus características.
Modelado de sistemas complejos
La lógica difusa se utiliza en el modelado de sistemas complejos para manejar la incertidumbre y la imprecisión en la descripción de los sistemas. Por ejemplo, en el modelado de un sistema de transporte público, la lógica difusa puede ser utilizada para determinar la frecuencia de los autobuses en función de la demanda y las condiciones del tráfico.
Beneficios de la lógica difusa
La lógica difusa ofrece varios beneficios en comparación con la lógica binaria tradicional. Algunos de estos beneficios son:
Manejo de la incertidumbre
La lógica difusa permite manejar la incertidumbre y la imprecisión en la toma de decisiones, lo que es especialmente útil en el mundo real, donde la mayoría de los problemas son inciertos e imprecisos.
Modelado de sistemas complejos
La lógica difusa permite modelar sistemas complejos de manera más efectiva que la lógica binaria, ya que permite una descripción más detallada y precisa de los sistemas.
Facilidad de uso
La lógica difusa es fácil de entender y utilizar, ya que utiliza términos y conceptos familiares para la mayoría de las personas.
Desafíos de la lógica difusa
Aunque la lógica difusa ofrece muchos beneficios, también presenta algunos desafíos. Algunos de estos desafíos son:
Complejidad computacional
La lógica difusa puede ser computacionalmente intensiva, especialmente cuando se utiliza para resolver problemas complejos.
Interpretación subjetiva
La lógica difusa requiere una interpretación subjetiva de las funciones de pertenencia, lo que puede dar lugar a diferentes resultados en función de la interpretación del usuario.
Falta de estandarización
La lógica difusa carece de una estandarización completa, lo que puede dificultar la comparación de resultados entre diferentes aplicaciones.
Conclusión
La lógica difusa es un enfoque innovador en la resolución de problemas que permite un razonamiento más cercano al pensamiento humano. Tiene aplicaciones en muchos campos, desde la ingeniería hasta la medicina, y ofrece varios beneficios en comparación con la lógica binaria tradicional. Sin embargo, también presenta algunos desafíos, como la complejidad computacional y la interpretación subjetiva. A pesar de estos desafíos, la lógica difusa es una herramienta valiosa para resolver problemas complejos en el mundo real.
Preguntas frecuentes
¿La lógica difusa es mejor que la lógica binaria tradicional?
Depende del problema que se esté resolviendo. La lógica difusa es mejor para problemas que implican incertidumbre e imprecisión, mientras que la lógica binaria es mejor para problemas que implican valores verdaderos o falsos.
¿La lógica difusa es fácil de entender y utilizar?
Sí, la lógica difusa es fácil de entender y utilizar, ya que utiliza términos y conceptos familiares para la mayoría de las personas.
¿La lógica difusa es computacionalmente intensiva?
Sí, la lógica difusa puede ser computacionalmente intensiva, especialmente cuando se utiliza para resolver problemas complejos.
¿La lógica difusa es adecuada para resolver problemas en el mundo real?
Sí, la lógica difusa es adecuada para resolver problemas en el mundo real, ya que permite manejar la incertidumbre y la imprecisión en la toma de decisiones.
¿La lógica difusa es una herramienta valiosa en la ingeniería?
Sí, la lógica difusa es una herramienta valiosa en la ingeniería, ya que permite modelar sistemas complejos de manera más efectiva que la lógica binaria.
Deja una respuesta