Descubre la lógica booleana con ejemplos prácticos

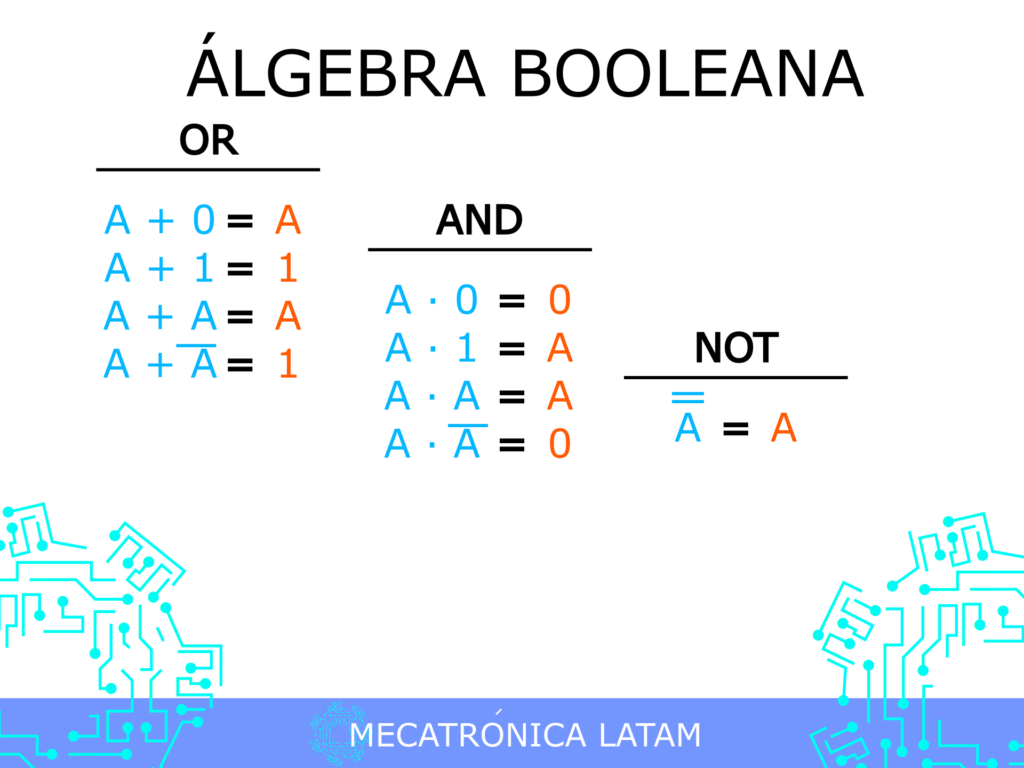
La lógica booleana es una herramienta fundamental en el mundo de la programación y la informática. Esta es una rama de la matemática que se encarga de estudiar las proposiciones lógicas y sus relaciones. Por eso, si quieres entender cómo funcionan muchas de las operaciones que se realizan en el mundo digital, es fundamental que aprendas a manejar la lógica booleana. En este artículo, te explicaremos qué es la lógica booleana y cómo puedes aplicarla en tu día a día, incluso si no eres programador.

¿Qué es la lógica booleana?

La lógica booleana se basa en dos valores lógicos: verdadero y falso (o 1 y 0). Estos dos valores son los que conforman las proposiciones lógicas, que son las que se utilizan para realizar operaciones lógicas. Por ejemplo, si decimos que "2 es mayor que 1", estamos haciendo una proposición lógica que es verdadera. En cambio, si decimos que "5 es menor que 4", estamos haciendo una proposición lógica que es falsa.

Operaciones lógicas básicas

Existen tres operaciones lógicas básicas que se utilizan en la lógica booleana: la negación, la conjunción y la disyunción.

Negación

La negación es la operación lógica que invierte el valor de una proposición. Por ejemplo, si tenemos la proposición "3 es mayor que 2", la negación de esta proposición sería "3 no es mayor que 2". En la lógica booleana, la negación se representa con el símbolo "~".

Conjunción

La conjunción es la operación lógica que devuelve verdadero únicamente si ambas proposiciones son verdaderas. Por ejemplo, si tenemos la proposición "2 es mayor que 1" y la proposición "3 es mayor que 2", la conjunción de estas dos proposiciones sería "2 es mayor que 1 y 3 es mayor que 2". En la lógica booleana, la conjunción se representa con el símbolo "^".

Disyunción

La disyunción es la operación lógica que devuelve verdadero si al menos una de las proposiciones es verdadera. Por ejemplo, si tenemos la proposición "2 es mayor que 1" y la proposición "3 es menor que 2", la disyunción de estas dos proposiciones sería "2 es mayor que 1 o 3 es menor que 2". En la lógica booleana, la disyunción se representa con el símbolo "v".

Ejemplos prácticos de lógica booleana

Ahora que ya conoces las operaciones lógicas básicas, vamos a ver algunos ejemplos prácticos de cómo se utilizan en el mundo de la programación.

Ejemplo 1: Validación de formularios

Supongamos que tienes un formulario en tu sitio web y quieres validar que los campos estén completos antes de enviarlos. Para hacer esto, puedes utilizar la lógica booleana. Por ejemplo, si tienes un campo para el nombre y otro para el correo electrónico, puedes hacer la siguiente validación:

```
if (nombre != "" && correo != "") {
// enviar formulario
} else {
// mostrar mensaje de error
}
```

En este caso, estamos utilizando la conjunción para validar que ambos campos estén completos. Si el nombre y el correo están completos, se enviará el formulario. Si no, se mostrará un mensaje de error.

Ejemplo 2: Búsqueda de elementos en una lista

Supongamos que tienes una lista de elementos y quieres buscar si un determinado elemento está presente en la lista. Para hacer esto, puedes utilizar la lógica booleana. Por ejemplo:

```
lista = [1, 2, 3, 4, 5]
elemento = 3

if (elemento in lista) {
// el elemento está en la lista
} else {
// el elemento no está en la lista
}
```

En este caso, estamos utilizando la disyunción para buscar si el elemento está presente en la lista. Si el elemento está en la lista, se ejecutará el primer bloque de código. Si no, se ejecutará el segundo bloque de código.

Ejemplo 3: Cambio de estado en un sistema

Supongamos que tienes un sistema que puede estar en dos estados: "encendido" o "apagado". Para cambiar el estado del sistema, puedes utilizar la negación. Por ejemplo:

```
estado = true

if (estado) {
estado = false
} else {
estado = true
}
```

En este caso, estamos utilizando la negación para cambiar el estado del sistema. Si el estado está en "encendido" (verdadero), se cambia a "apagado" (falso). Si está en "apagado", se cambia a "encendido".

Conclusión

Como has podido ver, la lógica booleana es una herramienta fundamental en el mundo de la programación y la informática. Si quieres entender cómo funcionan muchas de las operaciones que se realizan en el mundo digital, es fundamental que aprendas a manejar la lógica booleana. Con las operaciones lógicas básicas que te hemos explicado en este artículo, podrás empezar a aplicar la lógica booleana en tu día a día, incluso si no eres programador.

Preguntas frecuentes

1. ¿Es necesario saber programar para entender la lógica booleana?

No necesariamente. Aunque la lógica booleana es una herramienta fundamental en el mundo de la programación, también se puede aplicar en situaciones cotidianas, como la validación de formularios o la toma de decisiones.

2. ¿Qué pasa si aplico una operación lógica a valores que no son booleanos?

En general, si aplicas una operación lógica a valores que no son booleanos, el lenguaje de programación intentará hacer una conversión implícita de los valores a booleanos. Por ejemplo, en JavaScript, el valor 0 se considera falso y cualquier otro valor se considera verdadero.

3. ¿Existen más operaciones lógicas además de las tres básicas?

Sí, existen otras operaciones lógicas más complejas, como la implicación lógica, la equivalencia lógica, la disyunción exclusiva, entre otras.

4. ¿Qué es una proposición lógica?

Una proposición lógica es una afirmación que puede ser verdadera o falsa. Por ejemplo, "2 es mayor que 1" es una proposición lógica que es verdadera.

5. ¿Cómo se representan las operaciones lógicas en los lenguajes de programación?

Cada lenguaje de programación tiene su propia sintaxis para representar las operaciones lógicas. En general, se utilizan los símbolos ^ (conjunción), v (disyunción) y ~ (negación).