Descubre la lógica del mundo digital con la algebra booleana
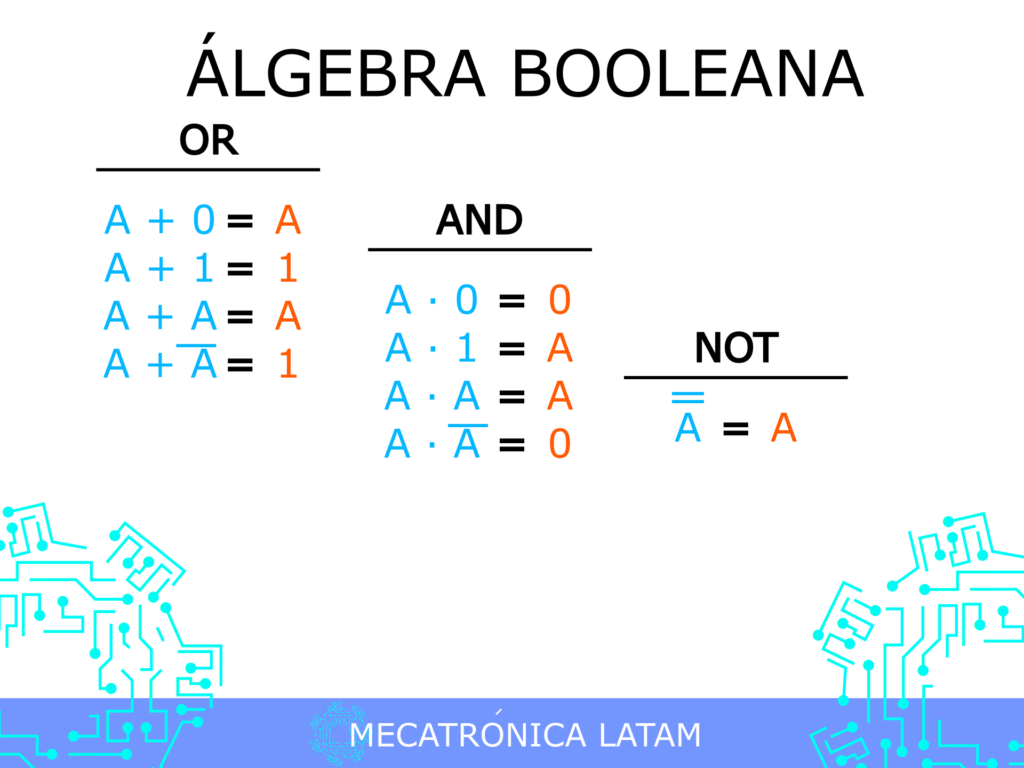
Si eres alguien que disfruta de la tecnología y se interesa por la manera en que funciona el mundo digital, es probable que hayas escuchado hablar sobre la algebra booleana. A primera vista, puede parecer un tema complicado, sin embargo, en este artículo te explicaremos de manera sencilla y con analogías la importancia de la algebra booleana en el mundo digital.
¿Qué es la algebra booleana?
La algebra booleana es una rama de las matemáticas que se encarga de estudiar las operaciones lógicas y las funciones booleanas. Su nombre se debe en honor a George Boole, un matemático inglés que desarrolló la teoría y las bases de la algebra booleana en el siglo XIX.
En el mundo digital, la algebra booleana se utiliza para representar y manipular información en forma de bits (0 y 1). A través de las operaciones lógicas, se pueden realizar diferentes combinaciones de bits y obtener resultados específicos.
¿Por qué es importante la algebra booleana en el mundo digital?
La algebra booleana es esencial para el funcionamiento de los circuitos digitales y los sistemas informáticos. En la actualidad, los dispositivos electrónicos están presentes en nuestra vida cotidiana y todos ellos utilizan la algebra booleana para realizar sus tareas.
Por ejemplo, cuando encendemos una computadora, se realizan una serie de operaciones lógicas que permiten que la máquina funcione correctamente. La algebra booleana también es utilizada en la programación y el desarrollo de software, ya que permite que las funciones y los algoritmos sean precisos y eficientes.
Operaciones lógicas básicas
Existen tres operaciones lógicas básicas que se utilizan en la algebra booleana: la negación, la conjunción y la disyunción.
Negación
La negación es una operación que cambia el valor de un bit. Si tenemos un bit con valor 0, al aplicar la negación obtendremos un bit con valor 1 y viceversa. En la tabla de verdad, la negación se representa con el símbolo ¬.
Ejemplo:
Si tenemos un bit con valor 0, al aplicar la negación obtendremos un bit con valor 1.
0 ¬0
1 ¬1
Conjunción
La conjunción es una operación que permite combinar dos bits. El resultado de la conjunción será 1 solamente si ambos bits tienen valor 1, en caso contrario, el resultado será 0. En la tabla de verdad, la conjunción se representa con el símbolo ∧.
Ejemplo:
Si tenemos dos bits, uno con valor 1 y otro con valor 0, al aplicar la conjunción obtendremos un bit con valor 0.
A B A ∧ B
0 0 0
0 1 0
1 0 0
1 1 1
Disyunción
La disyunción es una operación que permite combinar dos bits. El resultado de la disyunción será 0 solamente si ambos bits tienen valor 0, en caso contrario, el resultado será 1. En la tabla de verdad, la disyunción se representa con el símbolo ∨.
Ejemplo:
Si tenemos dos bits, uno con valor 1 y otro con valor 0, al aplicar la disyunción obtendremos un bit con valor 1.
A B A ∨ B
0 0 0
0 1 1
1 0 1
1 1 1
Aplicaciones de la algebra booleana en la tecnología
La algebra booleana se utiliza en diferentes áreas de la tecnología, aquí te presentamos algunas aplicaciones:
Circuitos lógicos
Los circuitos lógicos son dispositivos electrónicos que utilizan la algebra booleana para realizar operaciones lógicas. Estos circuitos se utilizan en diferentes dispositivos electrónicos, desde una calculadora hasta un teléfono celular.
Sistemas de control automático
Los sistemas de control automático utilizan la algebra booleana para tomar decisiones y realizar acciones. Por ejemplo, en un sistema de control de tráfico, se utilizan sensores para detectar la presencia de vehículos y se aplican operaciones lógicas para controlar los semáforos.
Programación de software
La programación de software utiliza la algebra booleana para la creación de algoritmos y la toma de decisiones en el software. La programación orientada a objetos también utiliza la algebra booleana para la creación de clases y objetos.
Conclusión
La algebra booleana es una herramienta esencial en el mundo digital. Permite que los dispositivos electrónicos funcionen correctamente y que los sistemas informáticos tomen decisiones precisas y eficientes. A través de las operaciones lógicas básicas, se pueden realizar diferentes combinaciones de bits y obtener resultados específicos. Si te interesa la tecnología, conocer sobre la algebra booleana te dará una comprensión más profunda sobre cómo funcionan los dispositivos electrónicos.
Preguntas frecuentes
¿Qué es un bit?
Un bit es la unidad básica de información en la computación. Representa un valor binario, 0 o 1, y es utilizado para almacenar y transmitir información.
¿Qué es una tabla de verdad?
Una tabla de verdad es una tabla que muestra los resultados de todas las combinaciones posibles de valores de entrada en una operación lógica.
¿Qué es la programación orientada a objetos?
La programación orientada a objetos es un paradigma de programación que utiliza objetos y clases para representar y manipular datos. Cada objeto es una instancia de una clase y tiene sus propias propiedades y métodos.
¿Qué es un circuito lógico?
Un circuito lógico es un dispositivo electrónico que utiliza la algebra booleana para realizar operaciones lógicas. Los circuitos lógicos se utilizan en diferentes dispositivos electrónicos, desde una calculadora hasta un teléfono celular.
¿Qué es un sistema de control automático?
Un sistema de control automático es un sistema que utiliza sensores y actuadores para controlar un proceso o una máquina de manera automática. Los sistemas de control automático utilizan la algebra booleana para tomar decisiones y realizar acciones.
Deja una respuesta