Domina el álgebra de Boole y simplifica tus operaciones
El álgebra de Boole es una herramienta matemática esencial para cualquier persona que trabaje con lógica digital, circuitos electrónicos y programación. Esta rama de las matemáticas se utiliza para simplificar las operaciones lógicas, lo que a su vez permite reducir la complejidad de los circuitos y los programas, mejorar la eficiencia y reducir los errores. En este artículo, te explicaremos todo lo que necesitas saber para dominar el álgebra de Boole y simplificar tus operaciones.
¿Qué es el álgebra de Boole?
El álgebra de Boole es una rama de las matemáticas que se centra en el estudio de las operaciones lógicas y los circuitos electrónicos. Esta herramienta matemática se basa en el uso de variables booleanas, que sólo pueden tener dos valores posibles: verdadero o falso (1 o 0). El álgebra de Boole se utiliza para simplificar y optimizar las operaciones lógicas y los circuitos electrónicos, lo que a su vez mejora la eficiencia y reduce los errores.
Operaciones básicas del álgebra de Boole
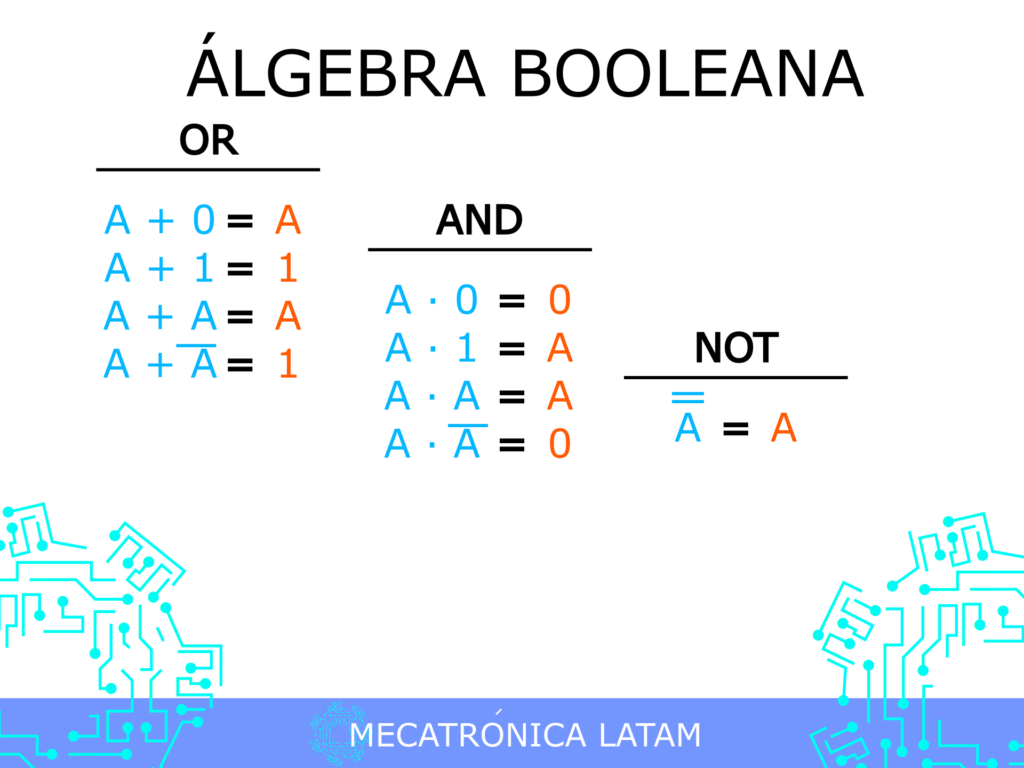
Las operaciones básicas del álgebra de Boole son la negación, la conjunción y la disyunción. La negación se utiliza para invertir el valor de una variable booleana. La conjunción se utiliza para obtener el valor verdadero sólo si ambas variables booleanas son verdaderas. La disyunción se utiliza para obtener el valor verdadero si al menos una de las variables booleanas es verdadera. Estas operaciones se representan mediante los símbolos de "not", "and" y "or" respectivamente.
Tabla de verdad
La tabla de verdad es una herramienta esencial del álgebra de Boole que se utiliza para representar y analizar las operaciones lógicas. En una tabla de verdad, se muestran todas las combinaciones posibles de valores para las variables booleanas, junto con el resultado de las operaciones lógicas correspondientes. Esta herramienta es muy útil para simplificar y optimizar las operaciones lógicas y los circuitos electrónicos.
Leyes de De Morgan
Las leyes de De Morgan son dos teoremas importantes del álgebra de Boole que permiten simplificar las operaciones lógicas complejas. La primera ley establece que la negación de una conjunción es equivalente a la disyunción de las negaciones de las variables booleanas. La segunda ley establece que la negación de una disyunción es equivalente a la conjunción de las negaciones de las variables booleanas. Estas leyes pueden simplificar significativamente las operaciones lógicas y reducir la complejidad de los circuitos y los programas.
Aplicaciones del álgebra de Boole
El álgebra de Boole tiene muchas aplicaciones en la vida cotidiana, especialmente en el campo de la electrónica y la informática. Se utiliza en el diseño de circuitos electrónicos, la programación de ordenadores, la criptografía y la seguridad informática, entre otros campos. El álgebra de Boole también es esencial para entender las operaciones lógicas detrás de los algoritmos y los programas informáticos.
Conclusión
El álgebra de Boole es una herramienta matemática esencial para cualquier persona que trabaje con lógica digital, circuitos electrónicos y programación. Esta rama de las matemáticas se utiliza para simplificar las operaciones lógicas, lo que a su vez permite reducir la complejidad de los circuitos y los programas, mejorar la eficiencia y reducir los errores. Si quieres simplificar tus operaciones y mejorar tu comprensión de la lógica digital, es esencial que domines el álgebra de Boole.
Preguntas frecuentes
¿Para qué se utiliza el álgebra de Boole?
El álgebra de Boole se utiliza para simplificar y optimizar las operaciones lógicas y los circuitos electrónicos, lo que a su vez mejora la eficiencia y reduce los errores. Esta herramienta matemática es esencial para cualquier persona que trabaje con lógica digital, circuitos electrónicos y programación.
¿Cuáles son las operaciones básicas del álgebra de Boole?
Las operaciones básicas del álgebra de Boole son la negación, la conjunción y la disyunción. La negación se utiliza para invertir el valor de una variable booleana. La conjunción se utiliza para obtener el valor verdadero sólo si ambas variables booleanas son verdaderas. La disyunción se utiliza para obtener el valor verdadero si al menos una de las variables booleanas es verdadera.
¿Qué es la tabla de verdad?
La tabla de verdad es una herramienta esencial del álgebra de Boole que se utiliza para representar y analizar las operaciones lógicas. En una tabla de verdad, se muestran todas las combinaciones posibles de valores para las variables booleanas, junto con el resultado de las operaciones lógicas correspondientes.
¿Qué son las leyes de De Morgan?
Las leyes de De Morgan son dos teoremas importantes del álgebra de Boole que permiten simplificar las operaciones lógicas complejas. La primera ley establece que la negación de una conjunción es equivalente a la disyunción de las negaciones de las variables booleanas. La segunda ley establece que la negación de una disyunción es equivalente a la conjunción de las negaciones de las variables booleanas.
¿En qué campos se utiliza el álgebra de Boole?
El álgebra de Boole tiene muchas aplicaciones en la vida cotidiana, especialmente en el campo de la electrónica y la informática. Se utiliza en el diseño de circuitos electrónicos, la programación de ordenadores, la criptografía y la seguridad informática, entre otros campos.
Deja una respuesta