Domina el álgebra booleana AND en pocos pasos
Si estás aprendiendo programación, es esencial que domines el álgebra booleana, especialmente el operador AND. Este operador permite a los programadores crear expresiones lógicas que evalúan si dos condiciones son verdaderas o falsas. Aunque puede parecer complejo al principio, dominar el álgebra booleana AND no es tan difícil como parece. En este artículo, te enseñaremos cómo hacerlo en unos pocos pasos.
¿Qué es el álgebra booleana AND?
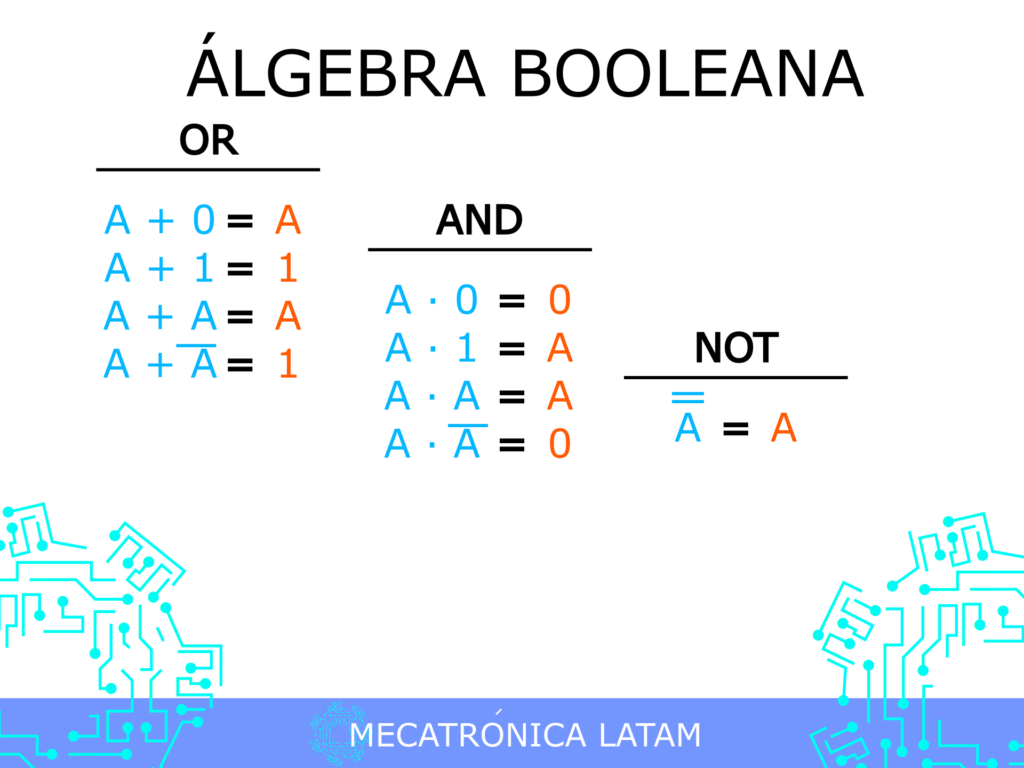
El álgebra booleana es un sistema matemático que se utiliza para representar la lógica booleana, es decir, la lógica que se basa en valores verdaderos o falsos. El operador AND es uno de los operadores booleanos más comunes. Este operador se utiliza para evaluar si dos condiciones son verdaderas o falsas.
Por ejemplo, si tienes dos variables, A y B, y quieres comprobar si ambas son verdaderas, puedes utilizar el operador AND. La expresión "A AND B" evaluará a verdadero solo si tanto A como B son verdaderas. Si una de las variables es falsa, la expresión evaluará a falso.
Pasos para dominar el álgebra booleana AND
A continuación, te mostramos algunos pasos sencillos que puedes seguir para dominar el álgebra booleana AND:
Paso 1: Comprender la tabla de verdad del operador AND
Antes de empezar a utilizar el operador AND, es importante que comprendas su tabla de verdad. La tabla de verdad muestra todos los posibles resultados de una expresión booleana en función de los valores de sus variables.
La tabla de verdad del operador AND es la siguiente:
| A | B | A AND B |
|---|---|--------|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
En esta tabla, A y B son las variables que se evalúan y A AND B es el resultado de la evaluación. Los valores 0 y 1 representan falsedad y verdad, respectivamente.
Paso 2: Utilizar el operador AND en expresiones lógicas
Una vez que comprendas la tabla de verdad del operador AND, puedes empezar a utilizarlo en expresiones lógicas. Por ejemplo, si tienes dos variables, A y B, y quieres comprobar si ambas son verdaderas, puedes utilizar la expresión "A AND B".
Paso 3: Combinar el operador AND con otros operadores booleanos
El operador AND se puede combinar con otros operadores booleanos para crear expresiones lógicas más complejas. Por ejemplo, puedes utilizar el operador NOT para negar una expresión lógica. La expresión "NOT(A AND B)" evaluará a verdadero si A y B son falsas.
También puedes utilizar el operador OR para crear expresiones lógicas que evalúen si al menos una de varias condiciones es verdadera. La expresión "A OR B" evaluará a verdadero si al menos una de las variables es verdadera.
Paso 4: Utilizar paréntesis para establecer el orden de evaluación
Cuando se combinan varios operadores booleanos en una expresión, es importante establecer el orden en que se evalúan las condiciones. Para hacerlo, puedes utilizar paréntesis. Las condiciones dentro de los paréntesis se evalúan primero.
Por ejemplo, la expresión "(A AND B) OR C" evalúa primero la condición "A AND B" y luego evalúa si el resultado es verdadero o si C es verdadero.
Conclusión
Dominar el álgebra booleana AND es esencial para cualquier programador. Siguiendo estos pocos pasos, puedes empezar a utilizar el operador AND y combinarlo con otros operadores booleanos para crear expresiones lógicas más complejas. Recuerda que la práctica es esencial para dominar cualquier habilidad, así que sigue practicando y experimentando.
Preguntas frecuentes
1. ¿Qué es el álgebra booleana?
El álgebra booleana es un sistema matemático que se utiliza para representar la lógica booleana, es decir, la lógica que se basa en valores verdaderos o falsos.
2. ¿Qué es el operador AND?
El operador AND es un operador booleano que se utiliza para evaluar si dos condiciones son verdaderas o falsas.
3. ¿Cómo se utiliza el operador AND en expresiones lógicas?
El operador AND se utiliza en expresiones lógicas para evaluar si dos condiciones son verdaderas. Por ejemplo, la expresión "A AND B" evaluará a verdadero solo si tanto A como B son verdaderas.
4. ¿Cómo se combina el operador AND con otros operadores booleanos?
El operador AND se puede combinar con otros operadores booleanos, como NOT y OR, para crear expresiones lógicas más complejas. Por ejemplo, la expresión "NOT(A AND B)" evaluará a verdadero si A y B son falsas.
5. ¿Por qué es importante dominar el álgebra booleana AND?
Dominar el álgebra booleana AND es esencial para cualquier programador, ya que permite crear expresiones lógicas que evalúan si dos condiciones son verdaderas o falsas. Esto es fundamental en la programación, donde las decisiones se basan en la evaluación de condiciones lógicas.
Deja una respuesta