6 razones trigonométricas esenciales: fórmulas y usos
¿Alguna vez te has preguntado cómo se utilizan las razones trigonométricas en la vida cotidiana? Las razones trigonométricas son una herramienta matemática esencial que se utiliza en muchas áreas, desde la ingeniería hasta la física y la navegación. En este artículo, te mostraremos las seis razones trigonométricas esenciales, sus fórmulas y usos.
- 1. Seno (sin)
- 2. Coseno (cos)
- 3. Tangente (tan)
- 4. Cotangente (cot)
- 5. Secante (sec)
- 6. Cosecante (csc)
- Conclusión
-
Preguntas frecuentes
- 1. ¿Por qué son importantes las razones trigonométricas?
- 2. ¿Cómo se utilizan las razones trigonométricas en la navegación?
- 3. ¿Por qué solo se aplican a los triángulos rectángulos?
- 4. ¿Cuál es la diferencia entre la tangente y la cotangente?
- 5. ¿Cómo se utilizan las razones trigonométricas en la física?
1. Seno (sin)
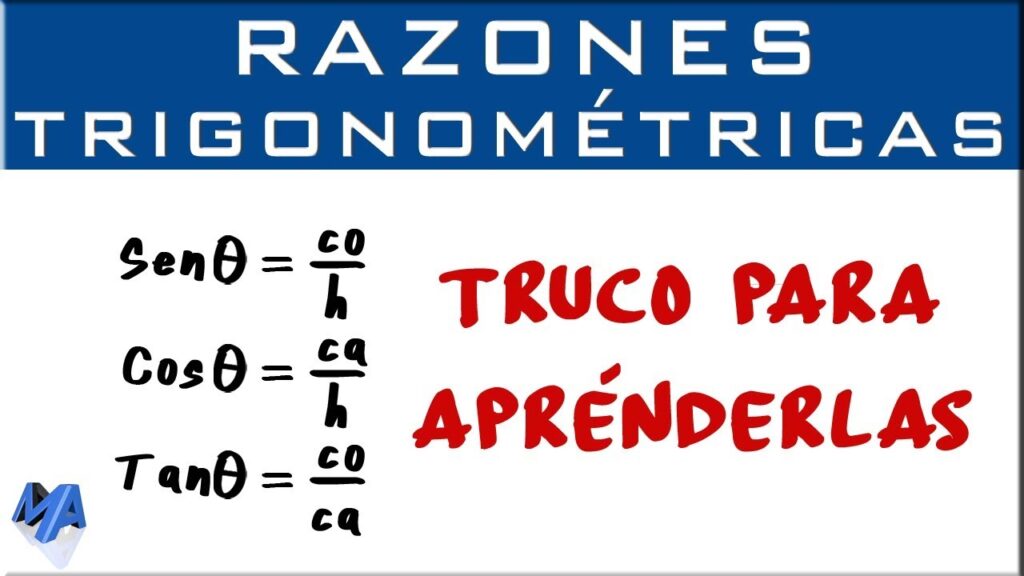
El seno es una de las razones trigonométricas más utilizadas. Se define como el lado opuesto dividido por la hipotenusa de un triángulo rectángulo. Su fórmula es:
sin(θ) = opuesto / hipotenusa
El seno se utiliza ampliamente en la geometría, la física y la ingeniería. Por ejemplo, se utiliza para calcular la altura de un edificio o la distancia entre dos objetos.
2. Coseno (cos)
El coseno también es una razón trigonométrica muy utilizada. Se define como el lado adyacente dividido por la hipotenusa de un triángulo rectángulo. Su fórmula es:
cos(θ) = adyacente / hipotenusa
El coseno se utiliza en la geometría y la física para calcular la longitud de una línea y la distancia entre dos puntos.
3. Tangente (tan)
La tangente es otra razón trigonométrica comúnmente utilizada. Se define como el lado opuesto dividido por el lado adyacente de un triángulo rectángulo. Su fórmula es:
tan(θ) = opuesto / adyacente
La tangente se utiliza en la física y la ingeniería para calcular la velocidad y la aceleración de un objeto.
4. Cotangente (cot)
La cotangente es la inversa de la tangente. Se define como el lado adyacente dividido por el lado opuesto de un triángulo rectángulo. Su fórmula es:
cot(θ) = adyacente / opuesto
La cotangente se utiliza en la física y la ingeniería para calcular la resistencia y la conductancia eléctrica.
5. Secante (sec)
La secante es la inversa del coseno. Se define como la hipotenusa dividida por el lado adyacente de un triángulo rectángulo. Su fórmula es:
sec(θ) = hipotenusa / adyacente
La secante se utiliza en la física y la ingeniería para calcular la impedancia eléctrica y la longitud de una línea.
6. Cosecante (csc)
La cosecante es la inversa del seno. Se define como la hipotenusa dividida por el lado opuesto de un triángulo rectángulo. Su fórmula es:
csc(θ) = hipotenusa / opuesto
La cosecante se utiliza en la física y la ingeniería para calcular la frecuencia y la longitud de onda de una onda electromagnética.
Conclusión
Las razones trigonométricas son una herramienta matemática esencial que se utiliza en muchas áreas, desde la ingeniería hasta la física y la navegación. En este artículo, te mostramos las seis razones trigonométricas esenciales, sus fórmulas y usos. Es importante tener en cuenta que estas razones trigonométricas solo se aplican a los triángulos rectángulos. Si deseas aplicar estas fórmulas a otros tipos de triángulos, deberás utilizar otras herramientas matemáticas.
Preguntas frecuentes
1. ¿Por qué son importantes las razones trigonométricas?
Las razones trigonométricas son importantes porque nos permiten calcular las medidas de los triángulos rectángulos y aplicarlas a problemas en la vida cotidiana.
2. ¿Cómo se utilizan las razones trigonométricas en la navegación?
Las razones trigonométricas se utilizan en la navegación para calcular la posición y el rumbo de un barco.
3. ¿Por qué solo se aplican a los triángulos rectángulos?
Las razones trigonométricas solo se aplican a los triángulos rectángulos porque estas razones se definen en términos de los lados de un triángulo rectángulo.
4. ¿Cuál es la diferencia entre la tangente y la cotangente?
La tangente se define como el lado opuesto dividido por el lado adyacente, mientras que la cotangente se define como el lado adyacente dividido por el lado opuesto.
5. ¿Cómo se utilizan las razones trigonométricas en la física?
Las razones trigonométricas se utilizan en la física para calcular la velocidad, la aceleración, la resistencia, la conductancia eléctrica, la impedancia eléctrica y la longitud de onda de una onda electromagnética.
Deja una respuesta